Types of triangles
Don’t be ‘obtuse’ – learn about the types of triangles and get the answers ‘right’ every time.
Author
Jill Padfield
Published:
Oct 2024
Key takeaways
- A triangle is one of the most important shapes in mathematics – Learning about triangles builds the foundation for more challenging subjects like geometry and trigonometry.
- There are different types of triangles – You can label a triangle by the size of its angles, the size of its sides, or both!
- To find the area of a triangle, you need its base and its height – Multiply the base and the height, then divide the number in half to get the triangle’s area.
Table of contents
Okay, we know we say every shape is important — and that is true! But if you’re looking for a shape that means serious business, look no further than the triangle.
Not only are there a number of different types of triangles, but calculating a triangle’s area and angles is a crucial part of solving many complex math problems in later mathematical subjects like precalculus and geometry.
Today, let’s take a closer look at what a triangle is, what properties define a triangle, and the different types of triangles you might encounter in 1st grade, 2nd grade, 3rd grade and beyond!
What is a triangle?
Easy: a triangle is a two-dimensional shape with three sides, three angles, and three vertices (the points where the sides connect). Because it has three or more sides, a triangle is also considered a polygon, so it belongs in the same shape family as the square, the rectangle, and even the decagon (which has ten sides!).
Triangles in the real world
Interestingly enough, there are not a lot of naturally occurring triangles out there. However, architects and contractors use triangles all the time when they’re building structures to help bear the load and make fantastic designs.
You might also notice that a Yield sign is shaped like a triangle. So is a clothes hanger and a billiards rack.
Parts of a triangle
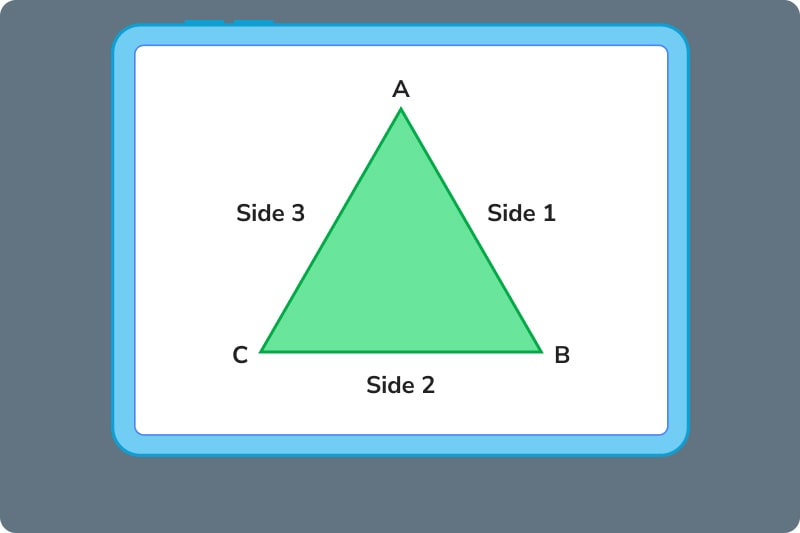
A triangle has several different parts. Let’s examine them together.
- A, B, and C are the triangle’s vertices, or where a side meets another side
- Inside the triangle, A, B, and C form angles that all measure 180° when added together
Types of triangles
There are a lot of different types of triangles. You can categorize a triangle using either its interior angles or the length of its sides – or both, in an ideal world!
Let’s look at how to categorize using angles first.
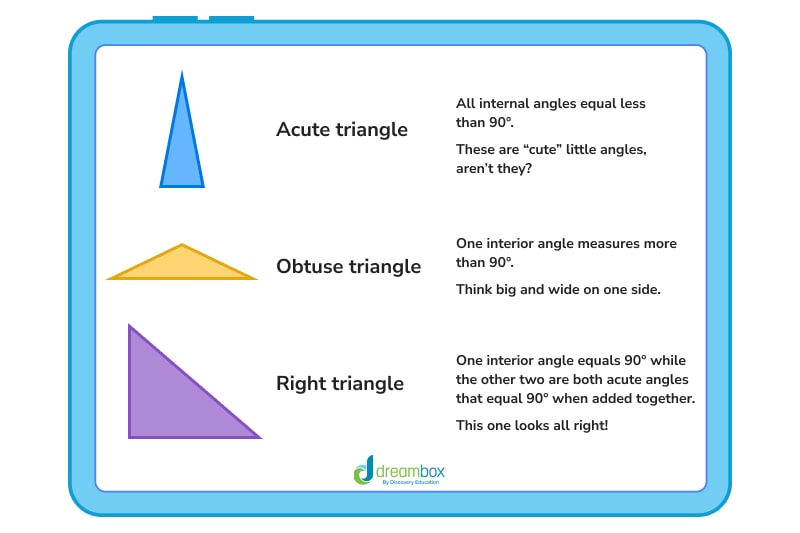
Triangles based on angles
There are three types of triangles named for the measure of their angles:
- Acute triangles
- Obtuse triangles
- Right triangles
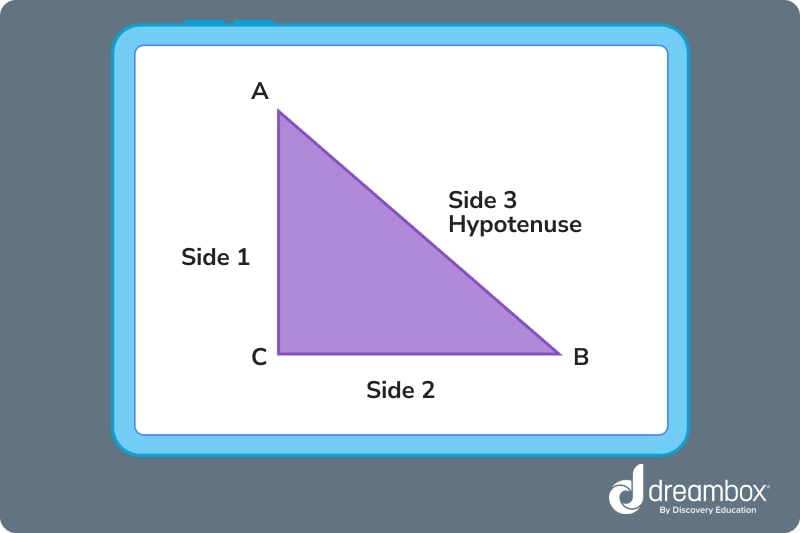
Right triangles
A right triangle has all the same parts as the isosceles triangle. However, there’s a fancy word for the name of the right triangle’s longest side: the hypotenuse.
In a right triangle, the base angle will always equal 90°. The other two angles will always equal 45° each, totaling 90° when added together.
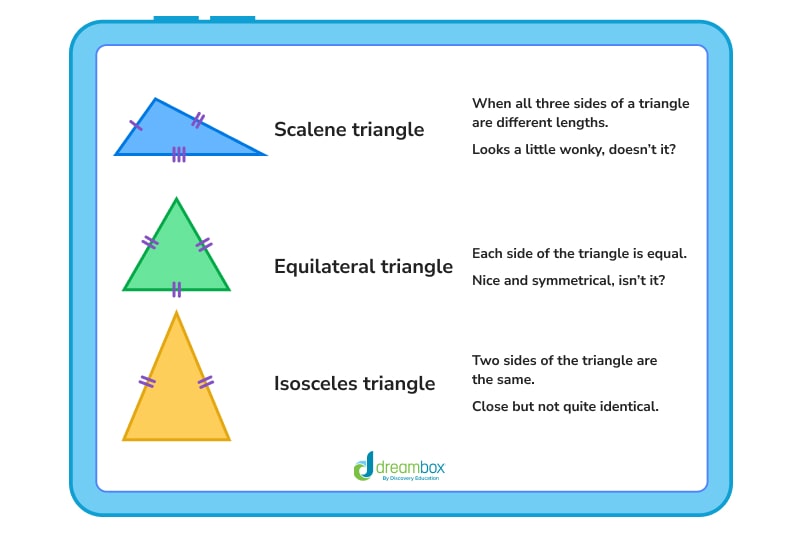
Triangles based on side length
There are also three types of triangles based on the length of their sides:
- Scalene triangles
- Equilateral triangles
- Isosceles triangles
Look at the hashes on each of the sides of the triangle. They tell you whether the measurements are all equal to each other or different.
Triangles based on both sides and angles
Of course, you can combine the two and have triangles labeled for both the length of their sides and their angles.
So, if you have a triangle with equal sides and all angles measure less than 90°, you have an acute equilateral triangle. If you have a triangle with one angle measuring more than 90° and two of three equal sides, you have an obtuse isosceles triangle, and so on and so forth.
Properties of a triangle
There are a few properties (think of them as rules) that a shape must have in order to be considered a triangle.
- A triangle must have three sides
- The sum of all interior angles must equal 180°
- The sum of the length of two sides is always greater than the length of the third side
- The area of a triangle is equal to half of the product of its base and height
What can we measure using the parts of a triangle?
We can measure both the perimeter and the area of a triangle. To calculate the perimeter of a triangle, simply add up the lengths of each of its sides.
So, if we are looking at a basic triangle with vertices labeled A, B, and C:
P = AB + AC + BC
But calculating the area of a triangle is a bit more complicated—and much more important when it comes to complex mathematics. Let’s learn together!
Area of a triangle
To determine the area of a triangle, we will need two basic measurements: the length of the triangle’s base and its height.
Now, you might think that you need to just measure the bottom of the triangle to find its base and one of its sides to find its height, but that isn’t true. Let’s break down finding a triangle’s area step-by step.
Finding the area of a triangle in 2 easy steps
1. Identify the height of a triangle
Split BC in half using figure D. Then, connect D to the triangle’s top vertex, A. Sometimes, the height will be drawn for you, like it is in the figure below. Sometimes, you will have to use your knowledge of right triangles and the formula for area (the Pythagorean theorem) to find the height.
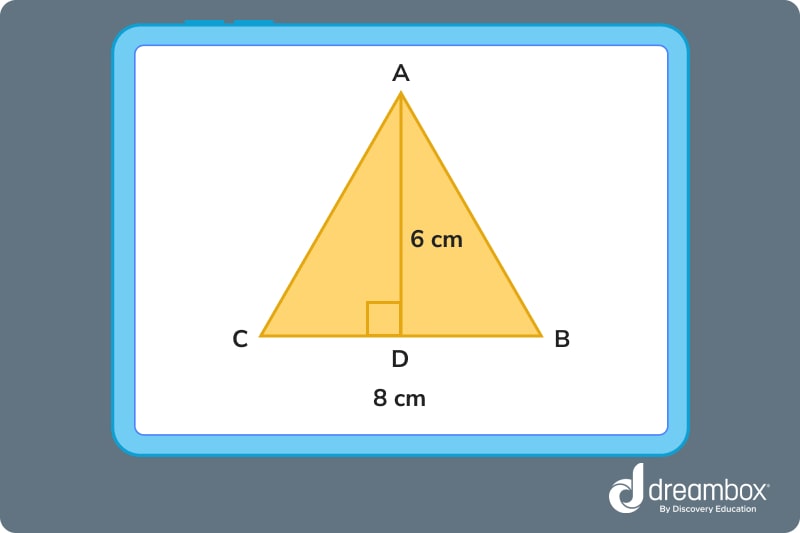
2. Use the formula A = ½ (base × height)
To calculate the area of a triangle, multiply the base and the height together, then divide by 2. In the example above, 8 × 6 = 48, so the area is 48 ÷ 2 = 24.
Let’s practice together
Now that we’ve had a chance to explore the types of triangles and how to calculate perimeter and area, let’s walk through a few practice problems together.
1. Which of the following is a right triangle?
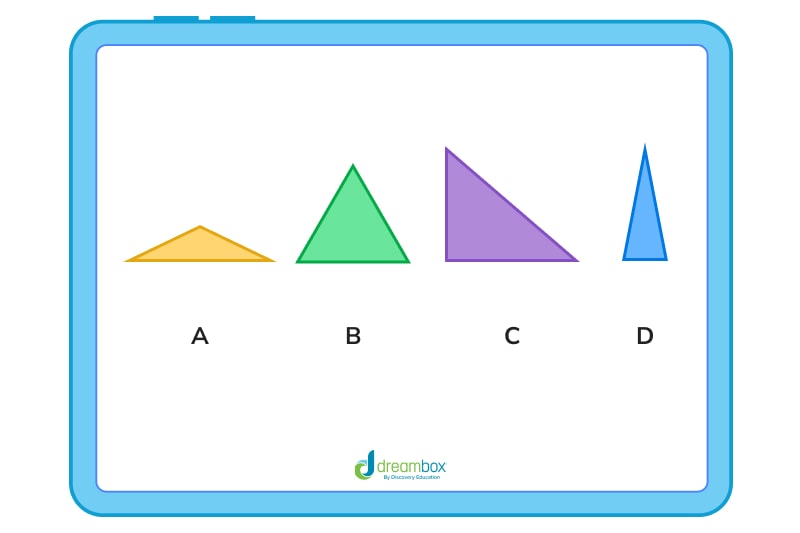
We know that right triangles have to have one right angle, one that measures 90°. The only triangle above that does that is C.
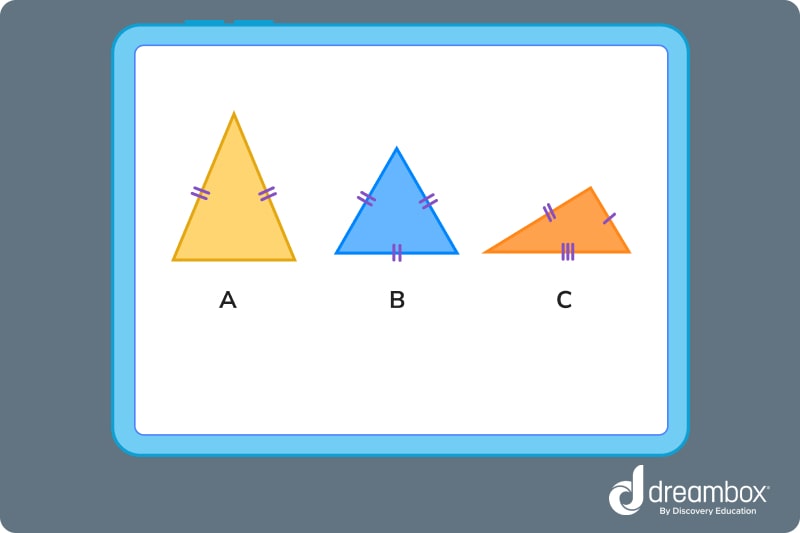
2. Which of the following is an isosceles triangle?
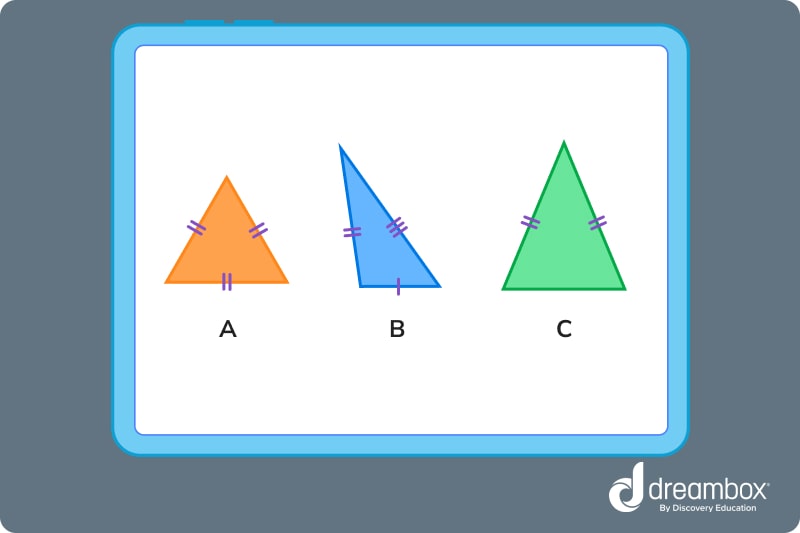
Since an isosceles triangle is equal on two of its three sides, the correct answer is A.
3. Find the area of a triangle with a base of 12 cm and a height of 8 cm.
So first, let’s calculate what the base × height is. 12 × 8 = 96.
So if the area is ½ of the base × height, then the triangle’s area is 48 cm.
Practice Problems
We’ve walked you through a few problems—now it’s time to practice on your own! Work through these problems and put your knowledge of triangles to the test.
Click to reveal the answer.
The answer is C.
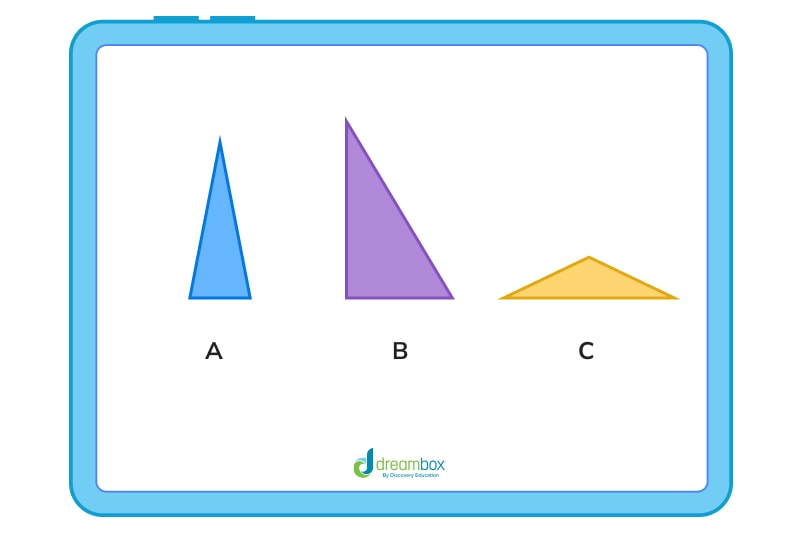
The answer is A.
The answer is C.
Parent Guide
-
1. The answer is C. How did we get here?
- 1. An obtuse triangle has at least one angle that is greater than 90°.
2. Triangle C has one angle that is greater than 90°. -
2. The answer is A. How did we get here?
- 1. An isosceles triangle has 2 equal sides, with a 3rd side that is a different length.
2. Using the hash marks, we can see that triangle A has 2 equal sides. Triangle B is an equilateral triangle, and triangle C is a scalene triangle. -
3. The answer is 36 cm. How did we get here?
- 1. A triangle’s area is equal to ½ of its base × its height.
2. 12 cm × 6 cm = 72 cm.
3. Half of 72 is 36 cm. -
4. The answer is 18 cm. How did we get here?
- 1. An equilateral triangle has equal sides.
2. That means that each side is 6 cm long.
3. 6 + 6 +6 or 6 × 3 = 18 cm -
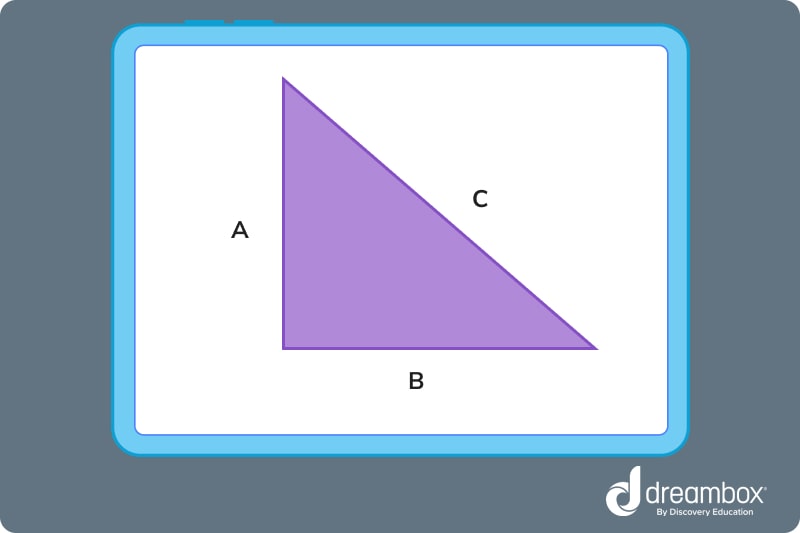
5. The answer is C. How did we get here?
- The hypotenuse of a right triangle is always its longest side.
FAQs about square shapes
There are three different triangle types labeled according to the length of their sides.
An equilaterial triangle has 3 equal sides.
An isocoles triangle has 2 equal sides.
A scalene triangle has 3 sides of differing lengths.
There are three different triangle types labeled according to the size of their angles.
In an acute triangle, at least one angle is less than 90°.
In a right triangle, one angle is exactly 90°.
In an obtuse triangle, at least one angle is greater than 90°.
To calculate the area of a triangle, you multiply the triangle’s base by its height, then divide that number by 2.
So if you have a triangle with a base of 16 cm and a height of 14 cm, you get 224 cm. Divide that number by 2, and the area of the triangle is 112 cm.
The Pythagorean theorem is an important equation in geometry. It is also how you find the hypotanuse of a right triangle. The actual equation is written as a2 + b2 = c2, with a being the measure of 1 side and b being the measure of the other side.
So if you had a right triangle with one side that measured 4 cm and another side that measured 8 cm, then to find the hypotenuse, you would calculate:
4 cm2 + 8 cm2 = c2
16 cm + 64 cm = 80
C (or the hypotenuse of the triangle) = √80, or 8.94 if you know your decimals!
