Prism shapes in math
Learn how to identify prism shapes by their properties and why they are important in math.
Author
Tess Loucka
Published:
March 2025
Key takeaways
- • Prisms are 3-D shapes characterized by having two identical, parallel bases and flat sides.
- • The shape of a prism’s base can be used to identify it.
- • Use the formula V = base (B) x height (H) to find the volume of a prism.
For most students, the introduction of 3-D shapes and prisms helps to bring mathematics into the real world, making it easier for young people to understand that numbers and shapes exist all around them.
Prisms are also important in many areas of life besides math, including science, construction, optics, architecture, design, art, and animation!
So, what are prisms in math? Let’s find out!
What is a prism shape?
A prism is a 3-D shape made of two identical and parallel bases connected by planes. A plane is a 2-D surface that can stretch infinitely in any direction.
The sides of a prism are called faces! All faces besides the bases are called lateral faces.
Faces connect to form edges and vertices.
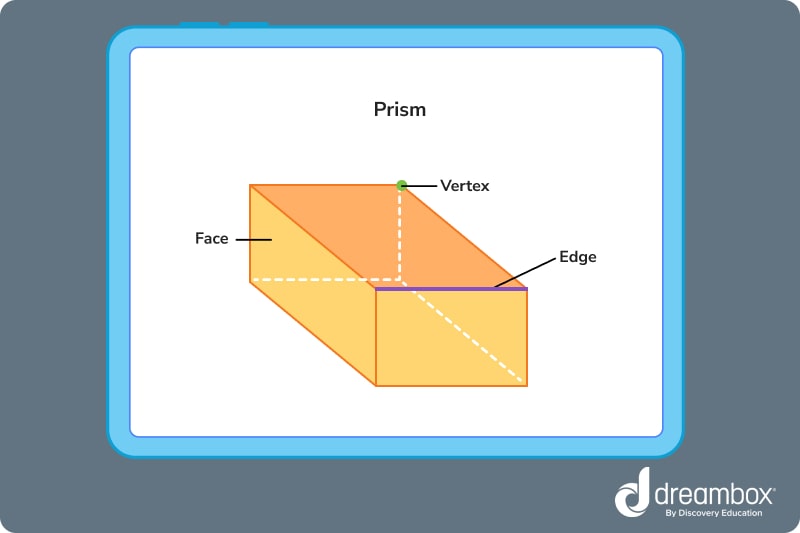
The base of a prism can be any polygon. As long as the shape has straight sides, it can form a prism.
Circles and ovals cannot create prisms because they have curved sides.
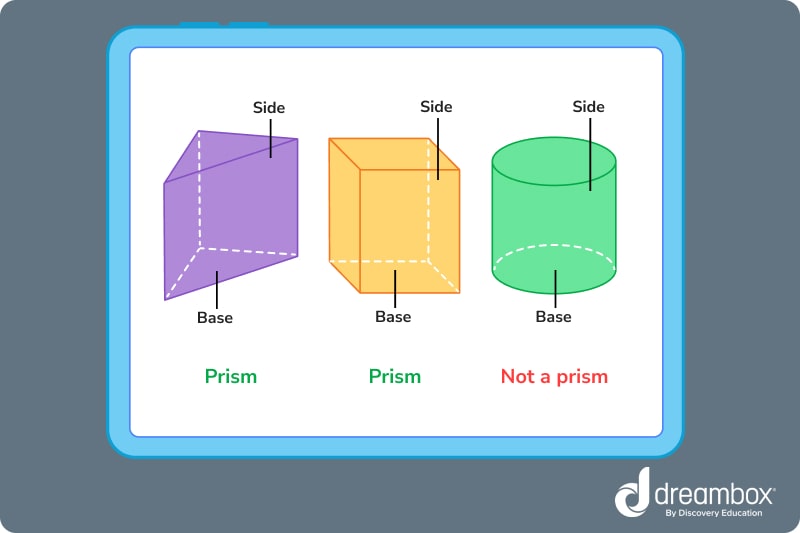
Prism-like shapes made of circles are called cylinders. These shapes should not be grouped with prisms as they have different properties.
Table of contents
Types of prisms
There are an infinite number of polygons and, therefore, an infinite number of prisms that can be made. The most common prisms are:
Rectangular prism
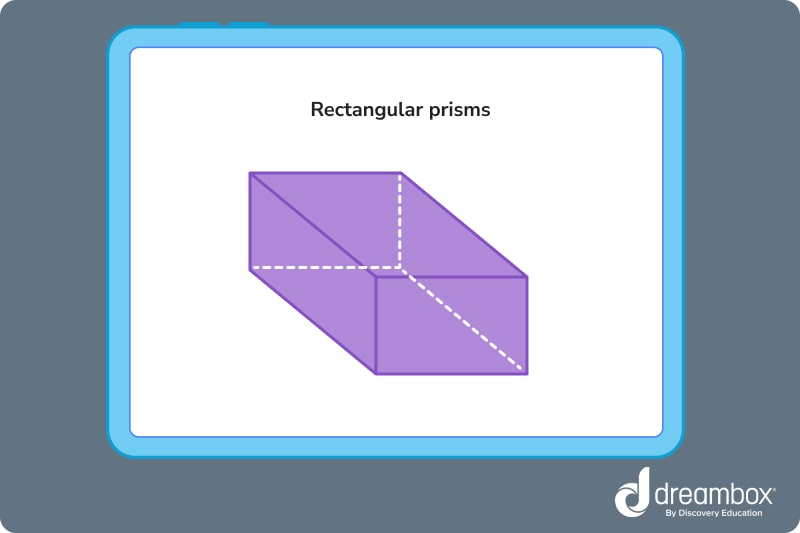
A rectangular prism is a 3-D shape with two identical and parallel rectangles on either side connected by 4 lateral faces. This shape is also called a cuboid.
Real-life examples of a rectangular prism include a shoebox, a refrigerator, a lunchbox, and a book! Can you think of any more examples?
Triangular prism
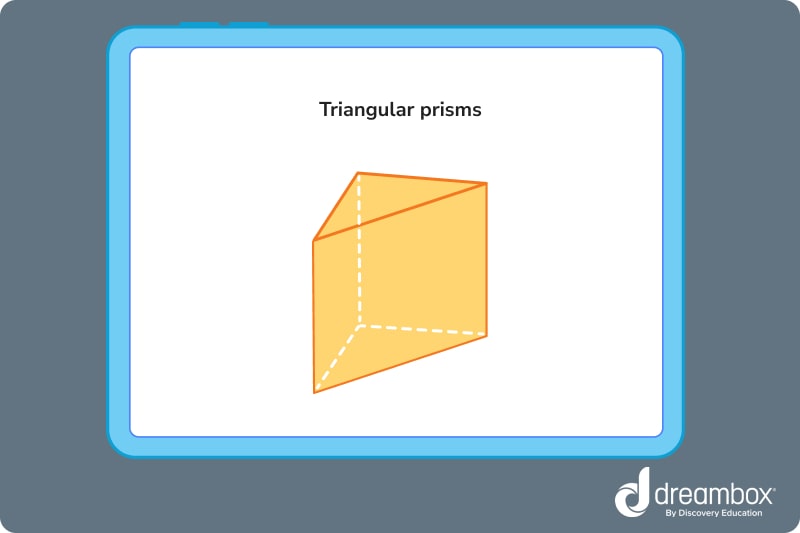
A triangular prism is a 3-D shape with two identical and parallel triangles on either side connected by 3 lateral faces.
Some real-life examples of a triangular prism include a camping tent, a triangular block of cheese, and a gabled roof. Can you think of other examples?
Square prism
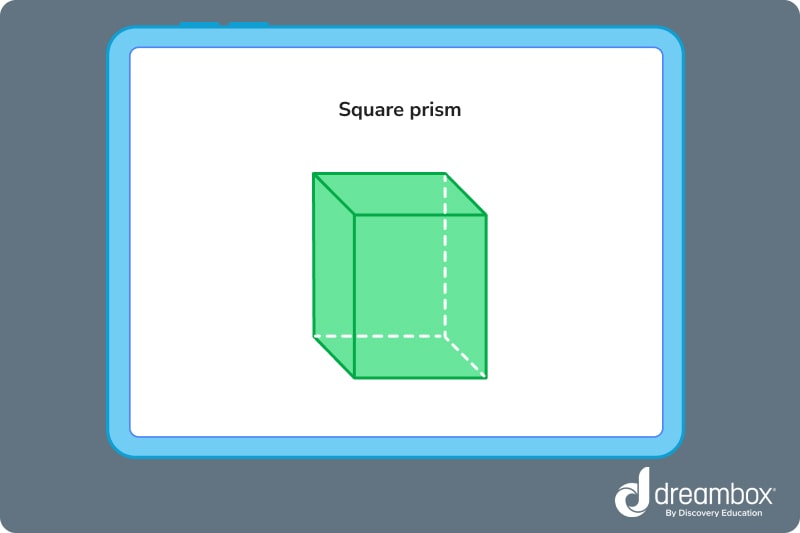
A square prism is a 3-D shape with two identical and parallel squares on either side connected by 4 lateral faces.
If all four lateral faces of a square prism are identical in height and length to the bases, a square prism is also called a cube.
Real-life examples of a square prism include dice and a Rubik’s Cube. Look around the room—are there any other examples you can think of?
How to identify prisms in math
Once you understand the rules of prisms, it is very easy to identify them when you come across one.
Let’s recap the criteria of all prisms:
- Prisms are 3-dimensional shapes.
- Prisms have two identical and parallel bases.
- Prisms are made up of flat surfaces.
If a shape meets these three criteria, it is a prism. To identify what type of prism it is, just look at the shape of the base. The shape of a prism’s base determines the prism’s name.
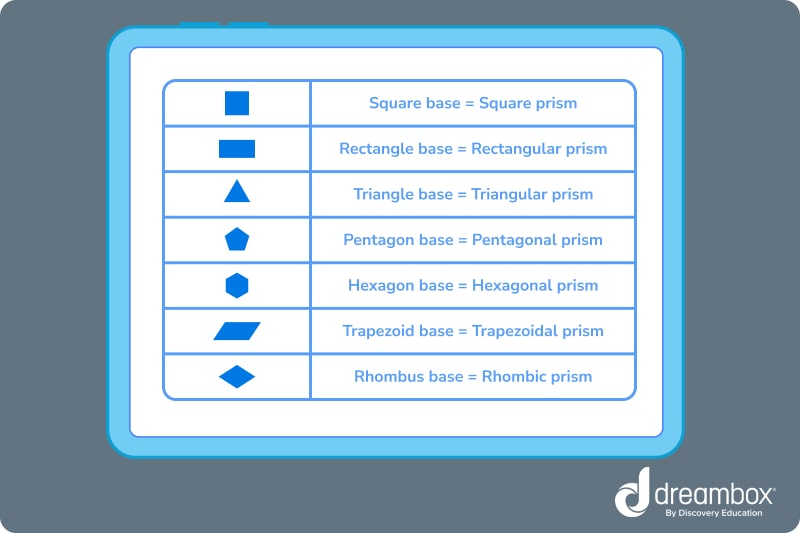
Working with prism shapes
Identifying prisms won’t be the only thing you have to do with prisms in math. Understanding how to create, label, and (very importantly) measure prisms is another skill you’ll want to have.
Finding the volume of a prism
Volume is defined as the amount of space a shape takes up or contains. When finding the volume of a shape, you are looking for the amount of space that exists within the shape’s borders. Volume is measured in cubic units.
The basic formula for finding the volume (V) of a prism is base x height (b x h). The B in this context represents the area of the prism’s base.
The formula you use to find the area of the base of a prism depends on the shape of the base.
To find the volume of a rectangular prism or square prism, we can simply use the formula V = length (L) x width (W) x height (H).
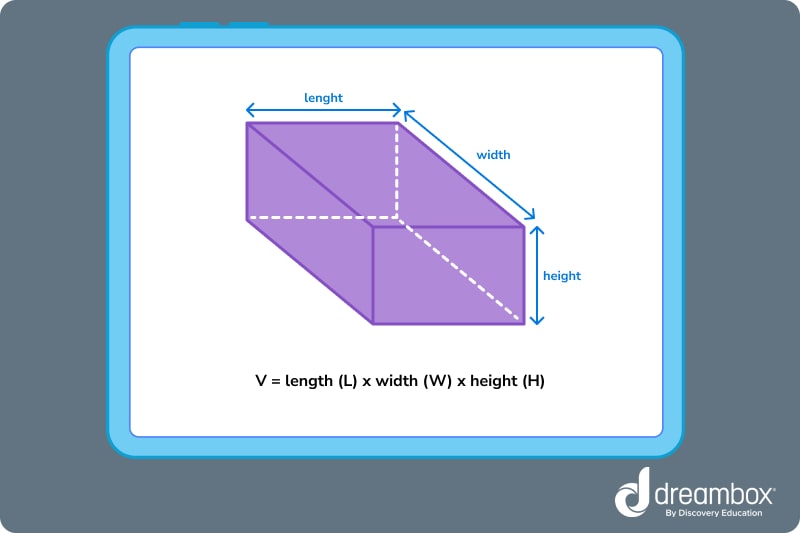
Now, how would we find the volume of this prism?
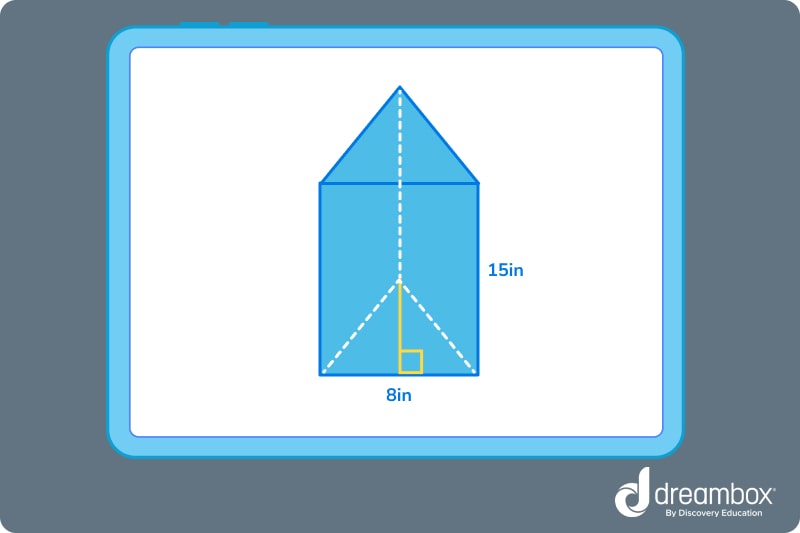
This is a triangular prism, so we cannot use the same formula we use for a square prism or rectangular prism. Find the area of the base first.
To find the area of a triangle, we must use the formula A = ½ x base (B) x height (H).
The base of the triangle is 8in and the height is 5in. We can write this out as A = ½ x 5 x 8. Therefore, A = 20.
Next, we multiply the area of the base with the height of the prism, which is 15in.
20 x 15 = 300.
This prism has a volume of 300 cubic inches.
Cross-sections of prisms
A cross-section is the shape created by slicing a 3-D shape with a flat plane. This shape is called a “slice,” “cross-section,” or “plane section.”
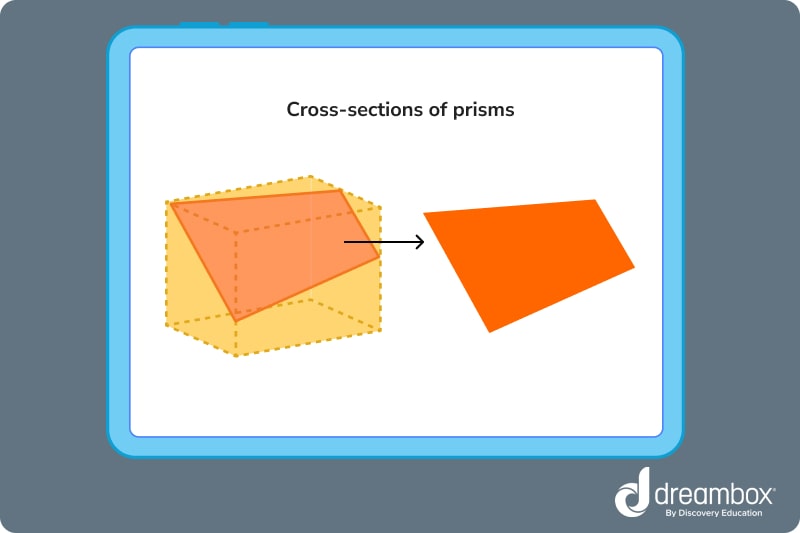
If a prism is sliced with a plane parallel to its base, the cross-section will be the same shape as the base.
Planes can slice through prisms at any angle, creating many different shapes depending on the number of sides the plane intersects. If a plane intersects 3 sides of a square prism, it can create a triangle. If it intersects all 6, it can create a hexagon.
Prism practice problems
Question 1: True or false: a cube is an example of a prism. Why or why not?
Answer: True. A cube is an example of a square prism because it is a 3-D shape, it has two identical, parallel bases, and only has flat surfaces.
Question 2: What is the volume of this prism?
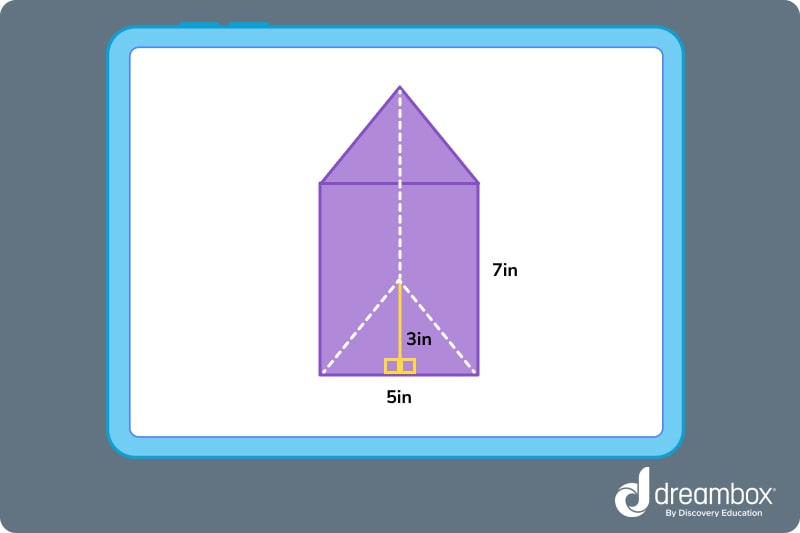
Answer: The volume of the prism is 52.5 cubic inches.
FAQs about prisms
A Rubik’s Cube, a brick, a camping tent, a lunchbox, and a pointed roof are all real-life examples of prisms.
The word ‘prism’ comes from the Latin word ‘prisma’ meaning ‘something sawed.’ It has been used to describe prism shapes since the 300s BC.
Students learn to identify prisms, as well as other 3-D shapes, in first or second grade. These shapes are used throughout mathematics for the rest of their education, becoming increasingly important during geometry courses.
Answer sheet
Question 1: A cube meets all the criteria of a prism and is, therefore, an example of a square prism.
Question 2: To find the volume of a prism, multiply the area of the base by the prism’s height. For this example, use the formula A = ½ x base (B) x height (H) to find the area of the triangular base. This becomes A = ½ x 5 x 3 = 7.5. Multiply this with the height of the prism — 7.5 x 7 = 52.5. Volume is written in cubic units.
