What is an Area Model in Math?
Area models are visual aids used to make multiplication and division problems simple.
Author
Amber Watkins
Published:
Oct 2024
Key takeaways
- • Fourth and fifth-grade math standards require students to be skilled multipliers.
- • Once your child becomes skilled in using area models, they will find it easier to divide and multiply multi-digit numbers.
- • When using an area model, you find the area in parts and add those parts together to find the sum.
Table of contents
What is an Area Model in Math?
Area models are visual aids used to make multiplication and division problems simple.
With area models, your child can:
1. Multiply two and three-digit numbers.
2. Divide two and three-digit numbers.
3. Multiply fractions and decimals.
First, let’s look at the big picture to see what area models look like and to understand the similarities between finding area and using area models, then we will see how they can be used to solve problems.
What is an Area Model?
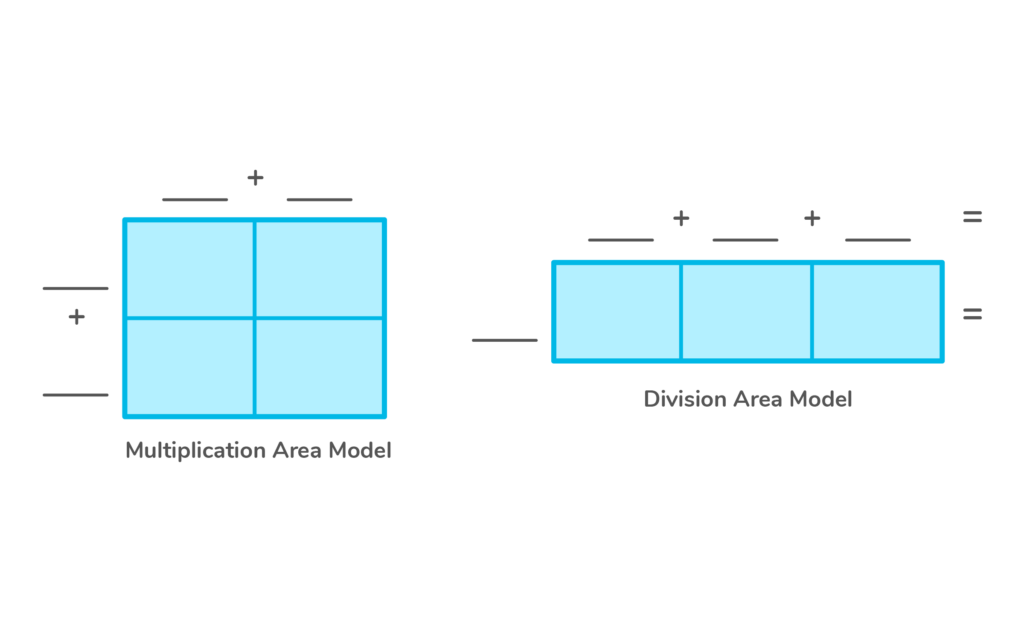
When you look at an area model, they are drawn as a square or a rectangle.
Fun Fact: Area models in square shape are called “square models.”
Since there are many similarities between finding the area of a square or rectangle and using these models to multiply or divide, they are called area models.
Multiplication Area Models
How do you find the area of a rectangle? Multiply the length times the width.
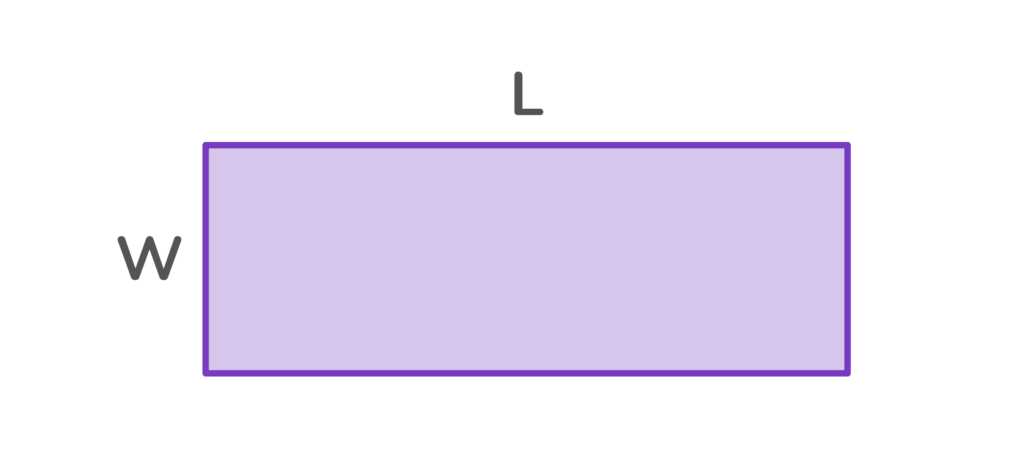
When using area models to multiply, one number is used as the length; the other number is used as the width.
Area models help you to find the area in parts which makes the problem easier to solve.
Division Area Models
What if you are given the area of a rectangle, but are missing a measurement for one of the sides? You divide the area by the side length.
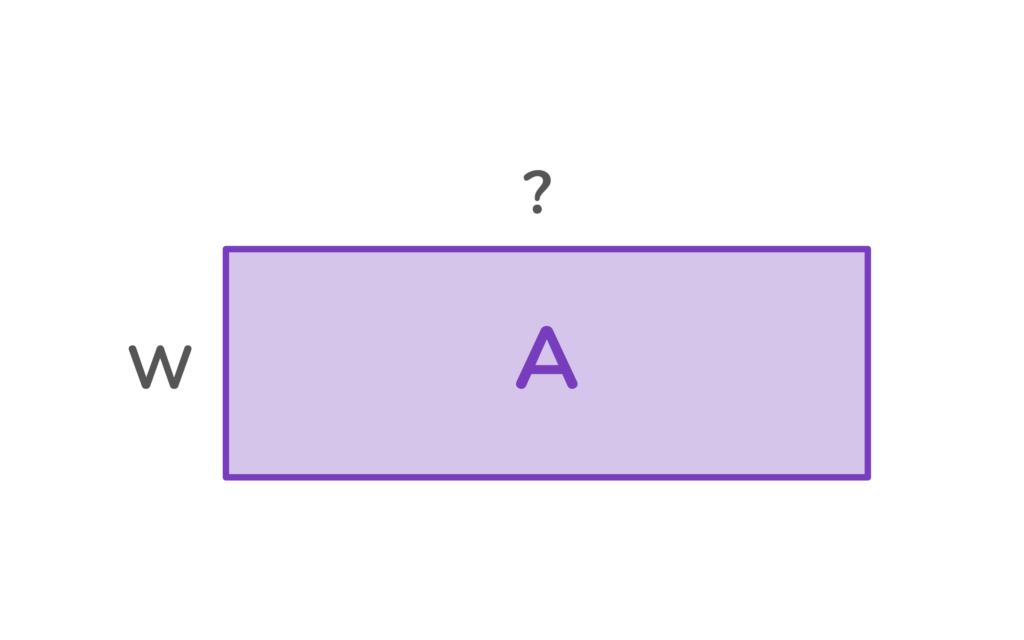
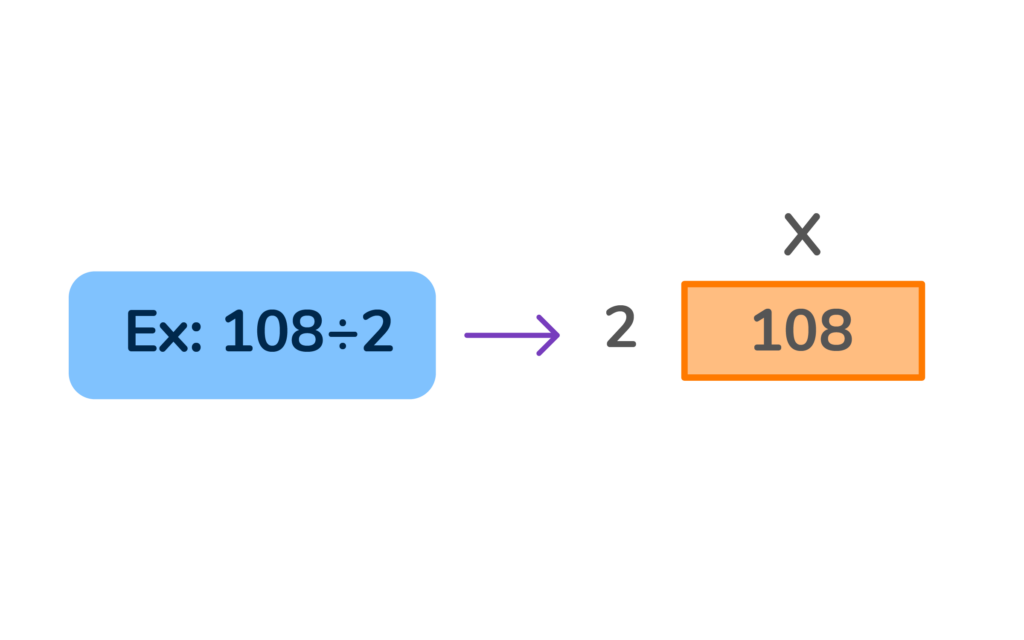
When dividing using area models, the dividend is the area, and the divisor is the length of one of the sides.
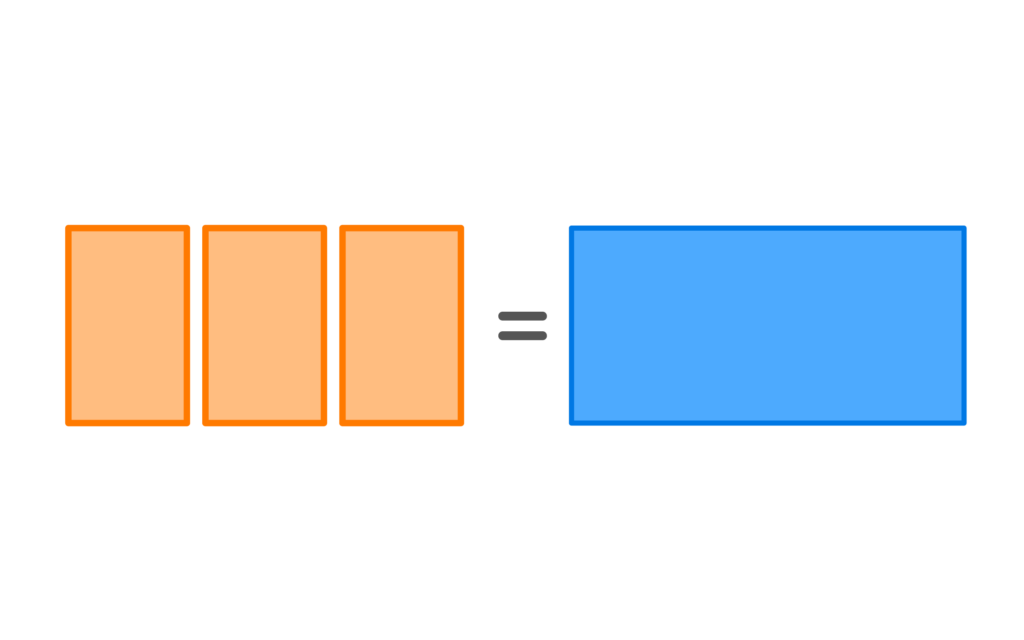
Area models help us divide the area into parts which makes finding the missing length easier.
How to Use an Area Model
Multiplying Using Area Models
Let’s see how to solve an area model multiplication problem.
What is 25 x 42?
We are going to use this multiplication area model to find the answer in parts.
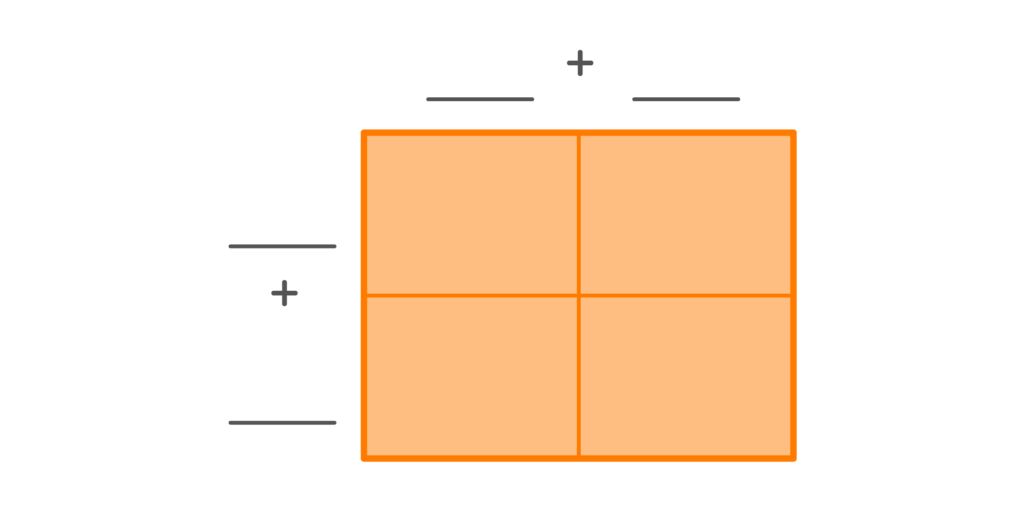
- First, we want to represent 25 on the top of the area model. So we write 25 in expanded form: 20 + 5.
- Next, we want to represent 42 on the side. So we write 42 in expanded form: 40 + 2.
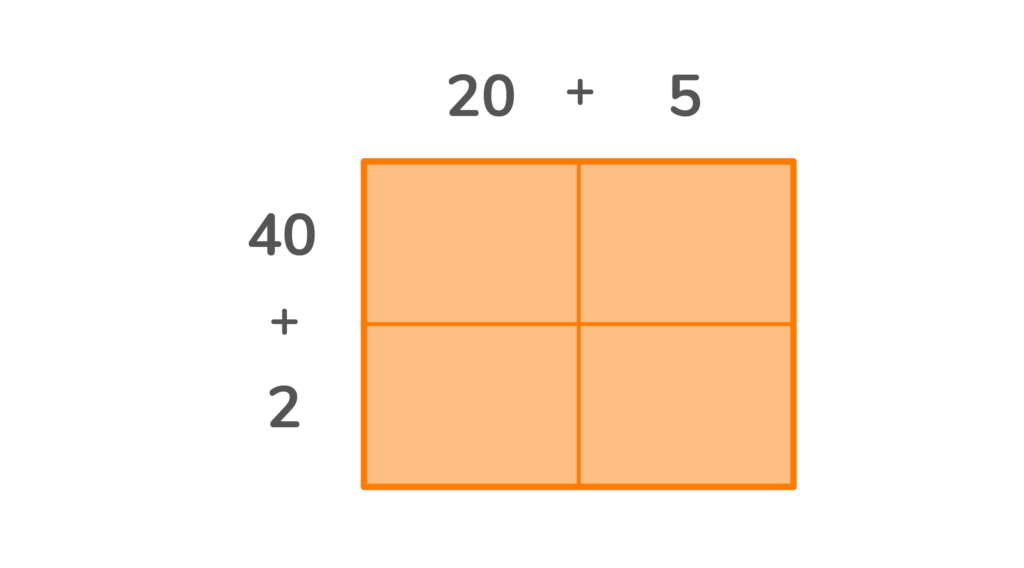
3. Now we have the numbers needed to multiply. Take each box and multiply the number above the column by the number before the row. (See the detailed illustration below).
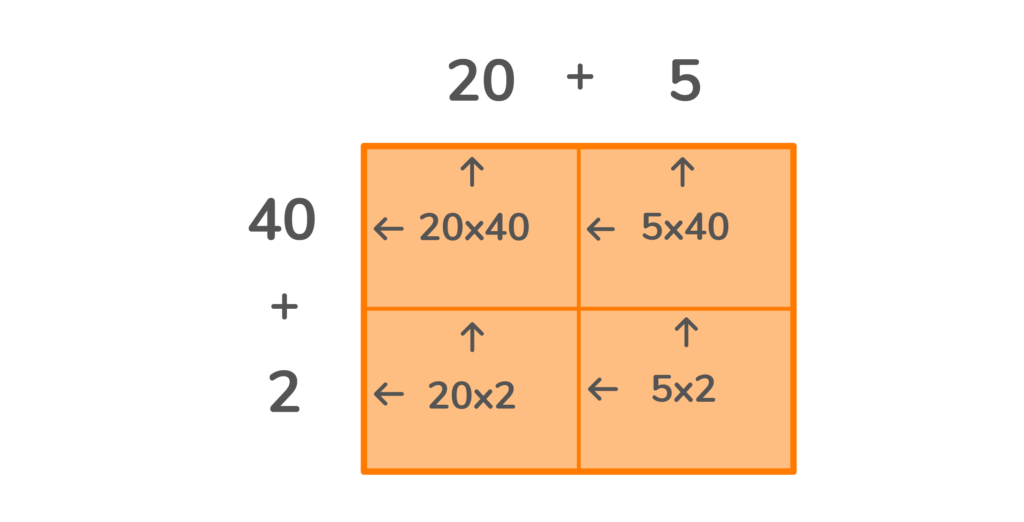
You will end up with one number in each of the four boxes.
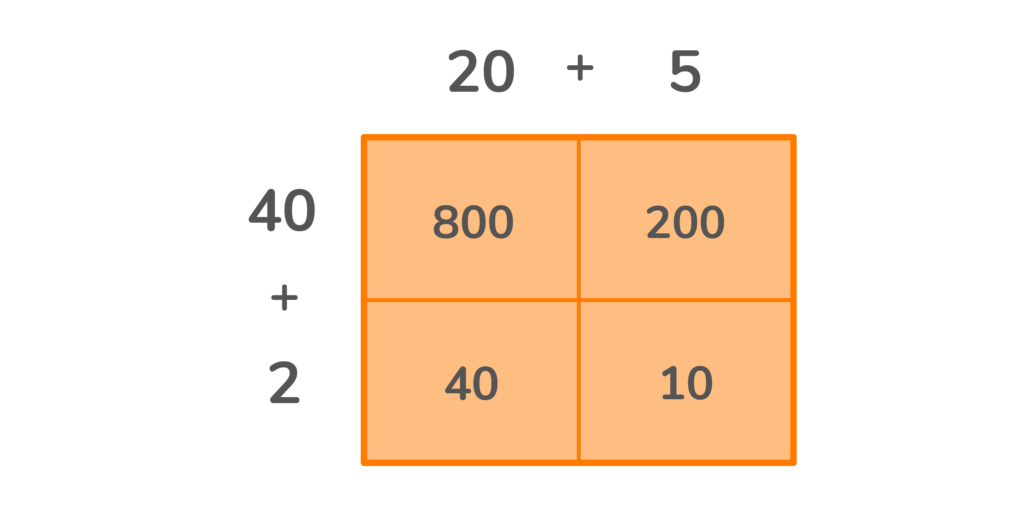
4. The final step is adding all the numbers together to find the answer.
800 + 200 + 40 + 10 = 1,050. So, 25 x 42 is equal to 1,050.
Dividing Using Area Models
Let’s see how to solve an area model division problem.
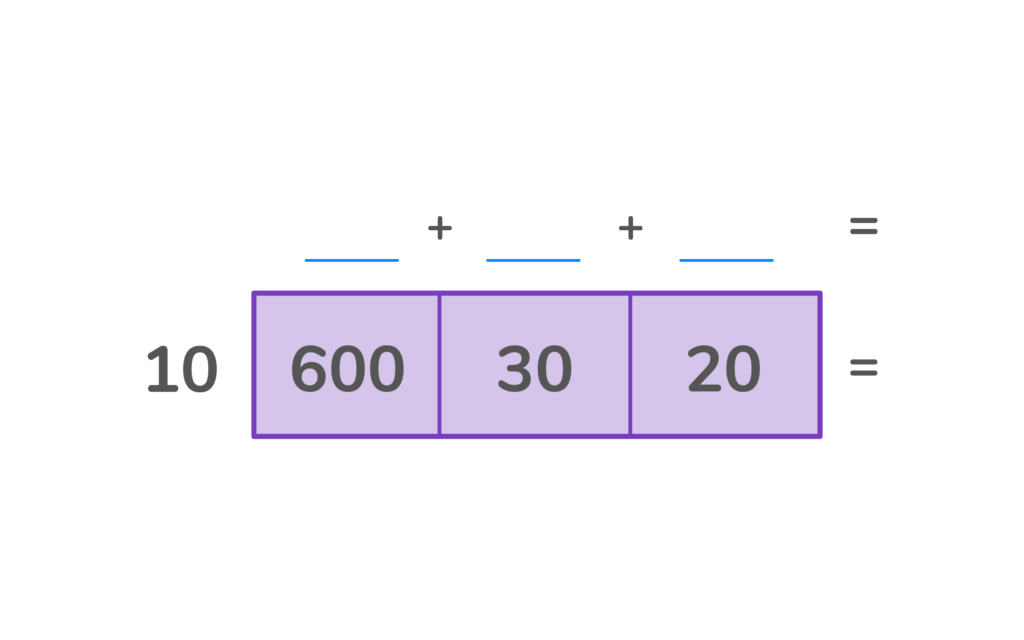
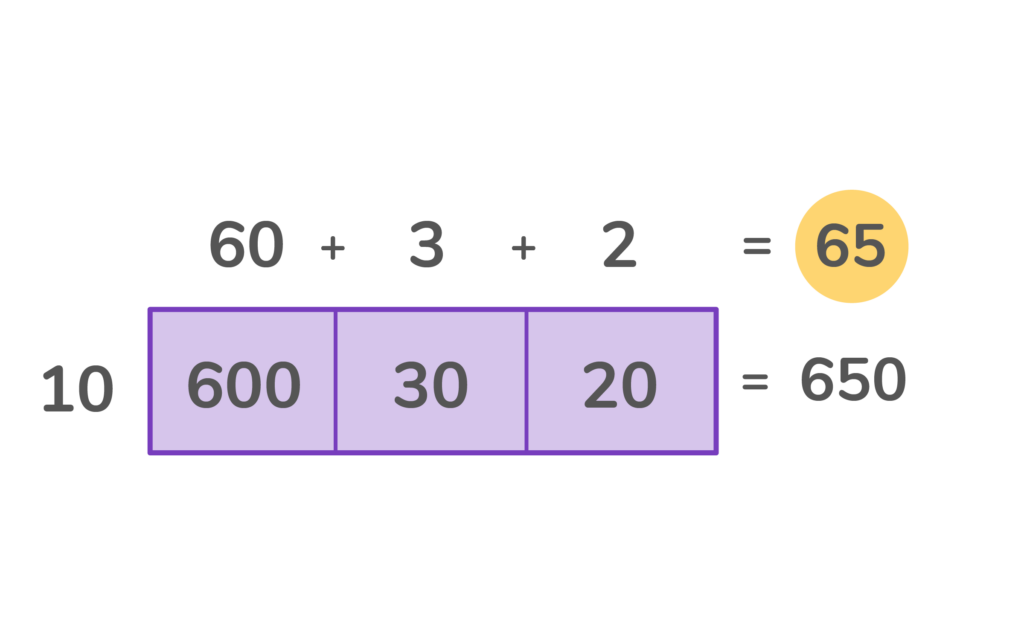
What is 650 / 10 =
We are going to use this division area model to find the answer in parts.
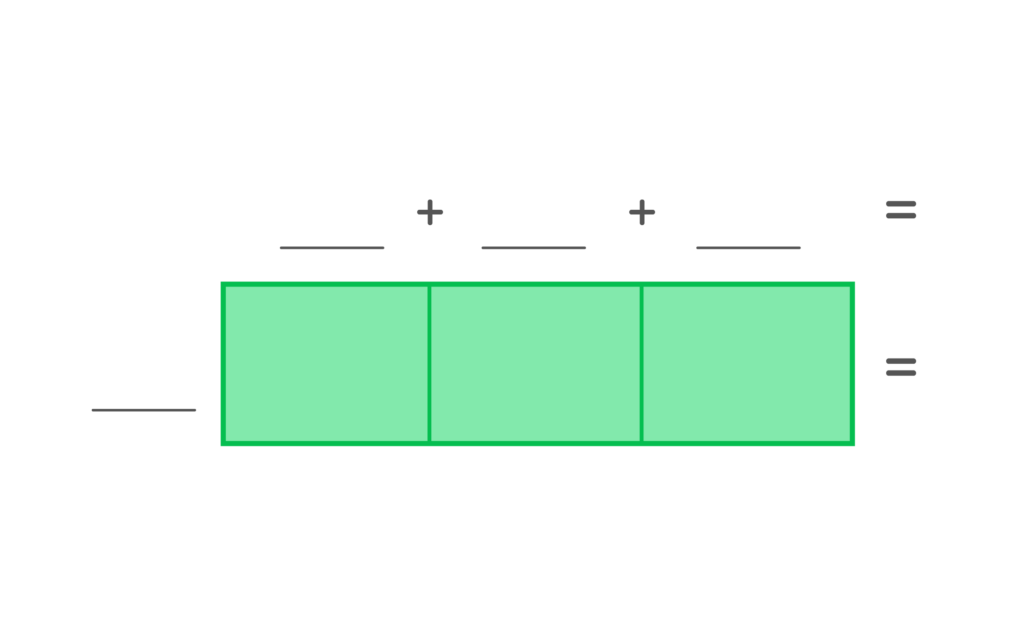
1. When dividing using area models, place the dividend inside the area model and the divisor on one side of the area model. Our answer will be at the top.
2. Choose three numbers that can be added to equal 650, 600 + 30 + 20. Place those three numbers inside the area model. Hint- all three numbers should be divisible by 10, the divisor.
You will end up with one number in each of the four boxes.
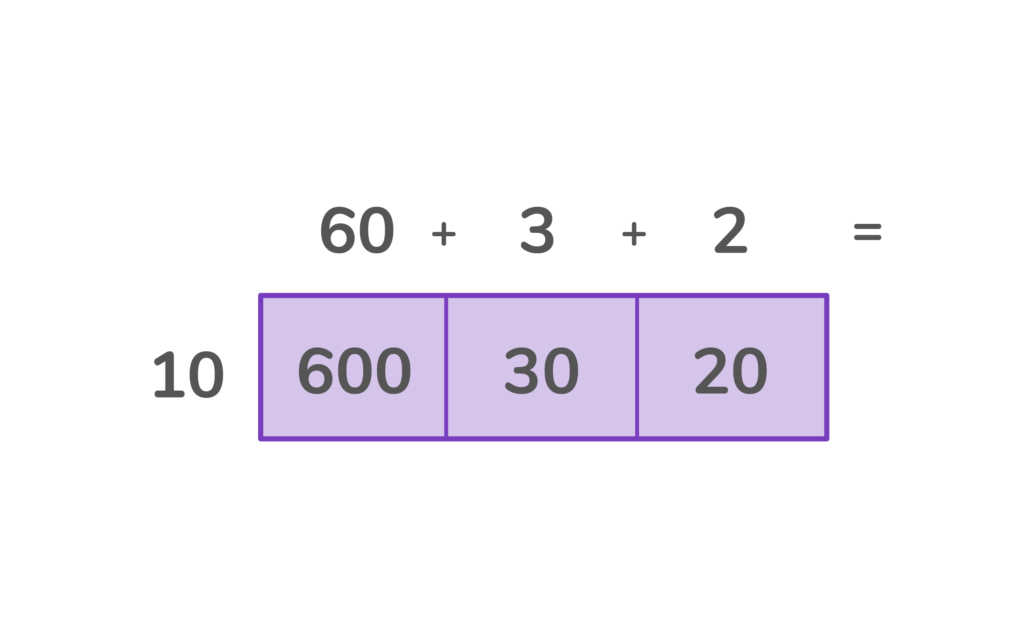
3. Finally, add the top numbers to find the missing length.
Practice Problems
Click on the boxes below to see the answers!
Answer: 62 x 13 = 806
Answer: 4.9 x 3.5 = 17.15
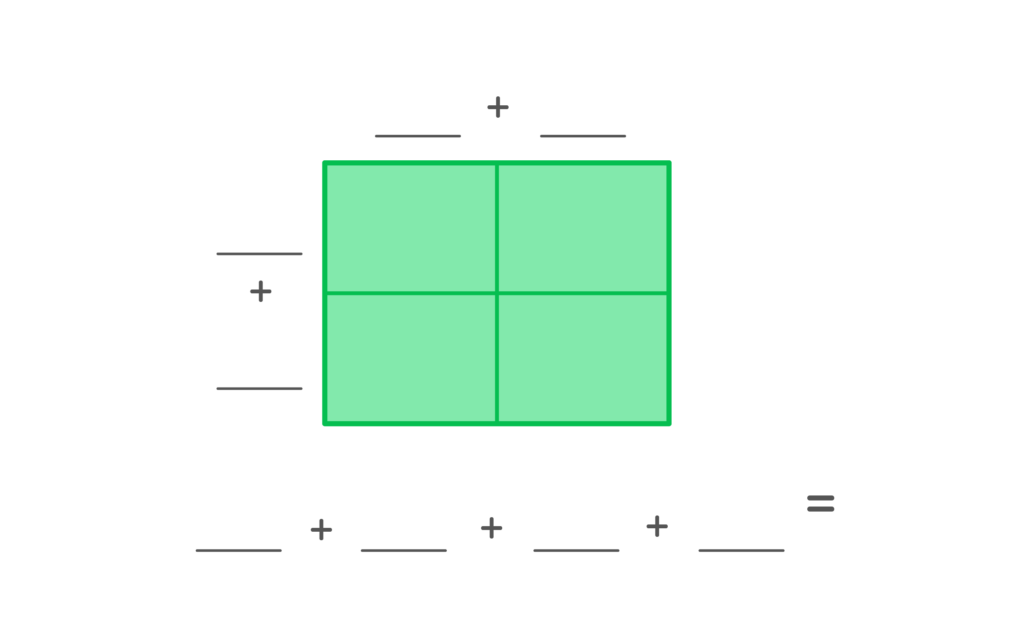
Answer: 180 / 12 = 15
FAQs About Area Models
Square models are area models used to multiply two-digit numbers.
Area models help you find the area in parts, this makes the problems easier to solve.
