What is an intersecting line?
Don’t be cross – understanding line intersection is easy when you know the basics!
Author
Tess Loucka
Published:
March 2025
Key takeaways
- • Intersecting lines are straight lines or line segments that share a common point.
- • Four angles will always be created by the intersection of two lines.
- • To find the point of interception of two lines, either graph them or set their equations equal to each other and solve for x and y.
Intersecting lines definition
Intersecting lines are any two or more lines that cross each other at a single point.
Think of the letter X. It is constructed by two lines that cross over each other at one common point. In other words, it is made up of two intersecting lines.
Intersecting lines are all around you, not only in the alphabet but in architectural designs, railroad tracks, roads, and even pairs of scissors!
Properties of intersecting lines
There are four basic properties of all intersecting lines.
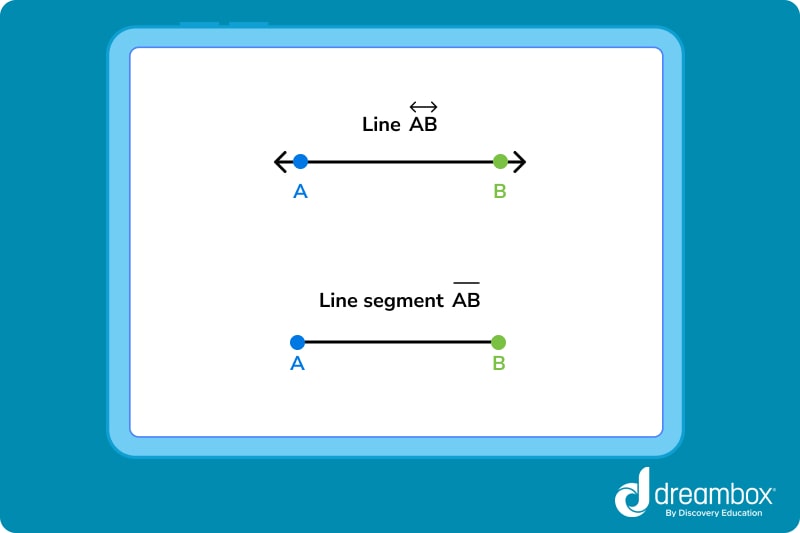
1. Intersecting lines must be either straight lines – indicated in math with arrows – or line segments – indicated with small circles on either end.
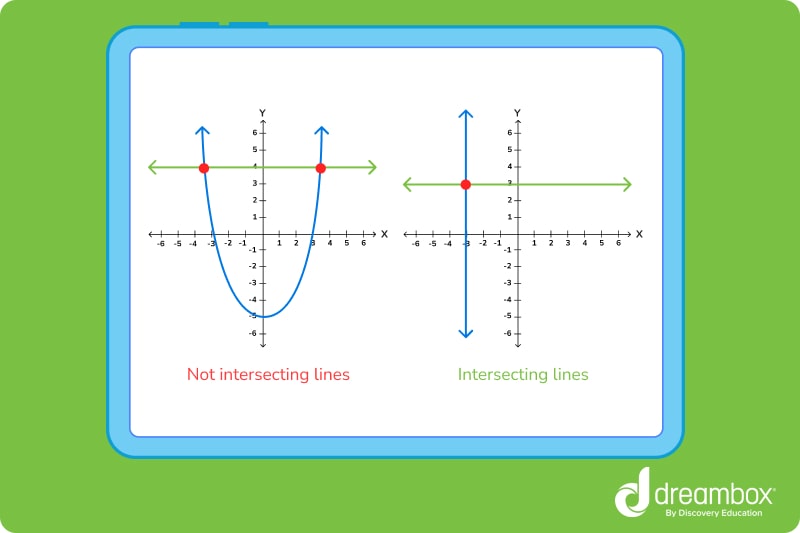
Non-intersecting lines are parallel lines. Parallel lines will always remain the same distance apart, never crossing.
2. Intersecting lines can only intersect each other at one point.
It is impossible for two straight lines to intersect each other more than once.
Curved or curvilinear lines can cross lines and line segments at multiple points. These are not classified as intersecting lines, although they do intersect.
3. The intersection of a line will always form four vertical angles.
These vertical angles are opposite angles and adjacent angles.
4. Two intersecting lines have different slopes.
Any two lines with different slopes will intersect at some point. Two lines with the same slope will never meet. They are parallel.
Table of contents
Examples of intersecting lines
Here is a basic example of an intersection of a line:
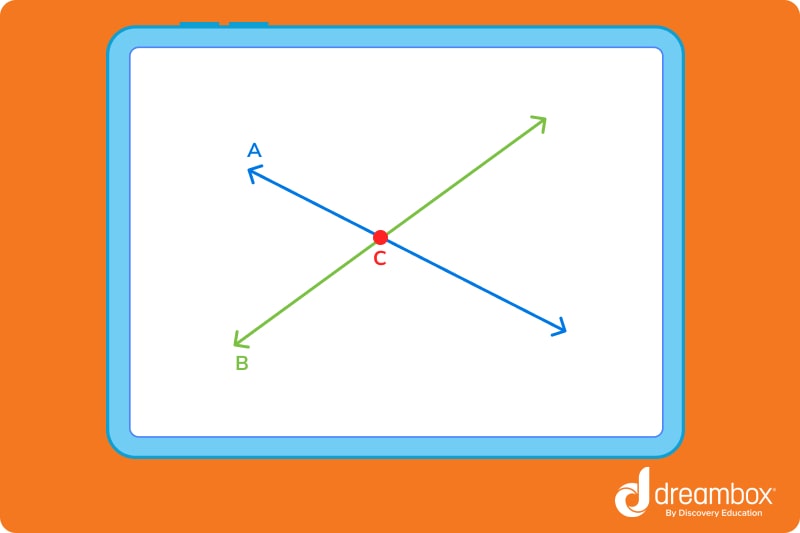
The point at which two lines intersect is called the line intersect or the point of intersection.
There is no limit to how many lines can cross at the same point of intersection. Two, 20, or even 2,000 lines can cross at one point.
Take a look at this example:
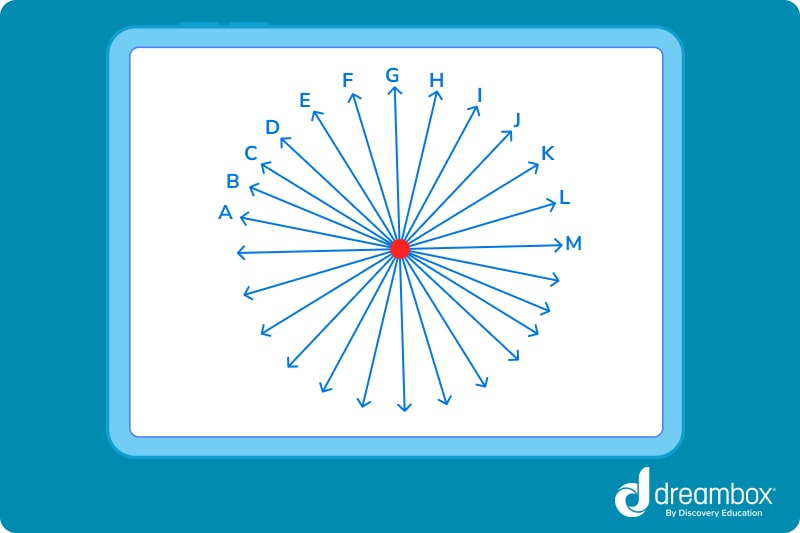
Intersecting lines can be crossed at multiple points by two or more lines, creating complex shapes like this:
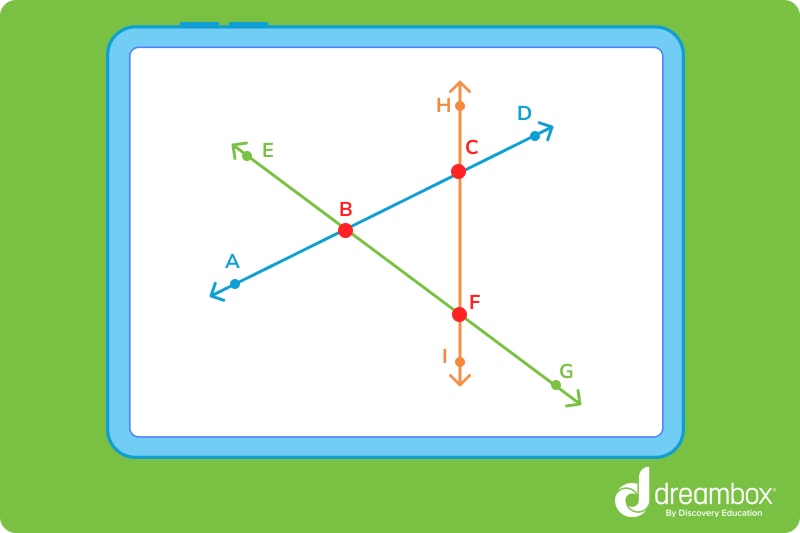
In this example, we have labeled the point of intersection and each line segment with letters. You can describe these intersections using geometric notation.
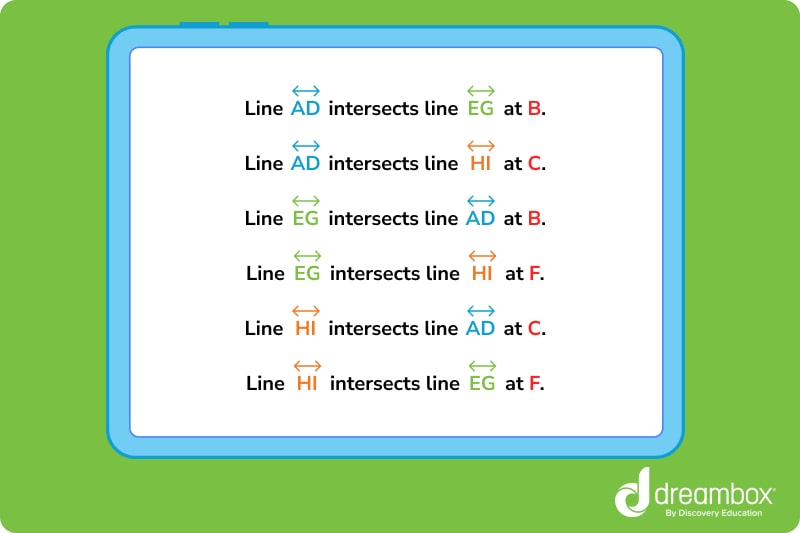
Angles formed by intersecting lines
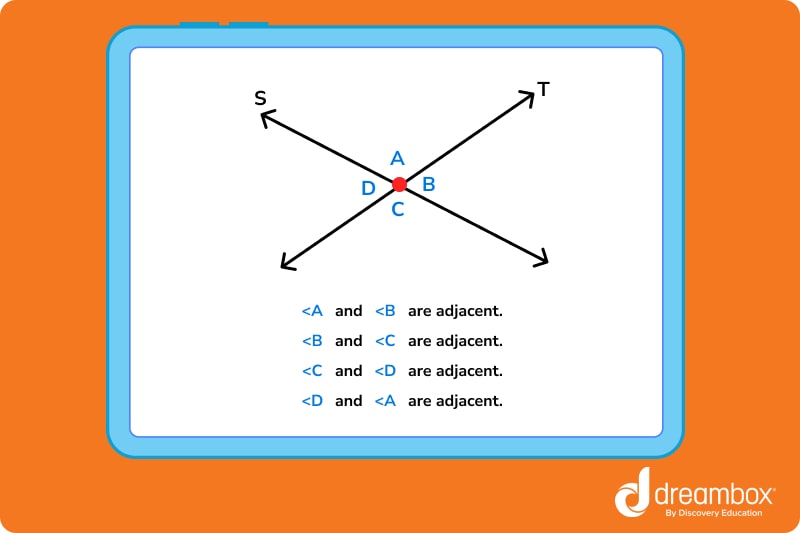
As stated above, every pair of intersecting lines will create four angles: adjacent angles and opposite angles.
Adjacent angles share a common side and vertex.
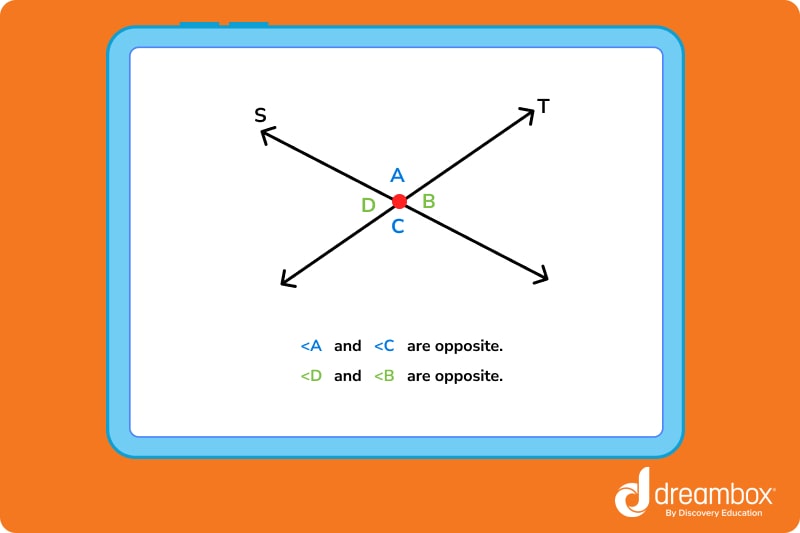
Opposite angles are two angles that sit across from each other on either side of two intersecting lines. Opposite angles always share the same measurements.
In the example below, < A and < B are adjacent because they share a side, made by line T, and a common vertex, made by the intersection of lines S and T.
In the same example, < A and < C are opposite, and < B and < D are opposite.
How to find the intersection of two lines
When dealing with intersecting lines, the point of intersection may not always be labeled. In some cases, you will be given the equation of two lines and must find the point of intersection yourself.
If you’re wondering how to find the intersection of two lines, this can be done either by graphing them or by working through their equations.
Here are the equations of two lines:
y = 2x – 1
y = 3x – 2
Since both lines equal y, using the rule of equality, we can conclude that 2x – 1 = 3x – 2. Now, solve for x.
Now that we know x = 1, we can replace x in one of the original equations to solve for y.
Since x = 1 and y = 1, we now know that the point of intersection of these two lines is (1,1).
But what if the two equations don’t both equal y?
In this case, the first step is to make them equal y by reordering their equations.
Here are the equations of two lines:
y + 8 = 3x
y = -4x + 6
Let’s rearrange the first equation so it equals y.
Now that both equations equal y, let’s set them equal to each other and solve for x.
Now that we know x = 2, we can plug 2 in for x in one or both of the original equations to solve for y.
So, y = -2 and x = 2. Therefore, the point of intersection of these two lines is (2,-2).
For more practice with intersecting lines, the intersecting lines definition, angles, and finding points of intersection, use a math practice website or study guide to find additional practice problems, detailed answer keys, and explanations.
Practice problems
Question 1: Does the image below show two intersecting lines?
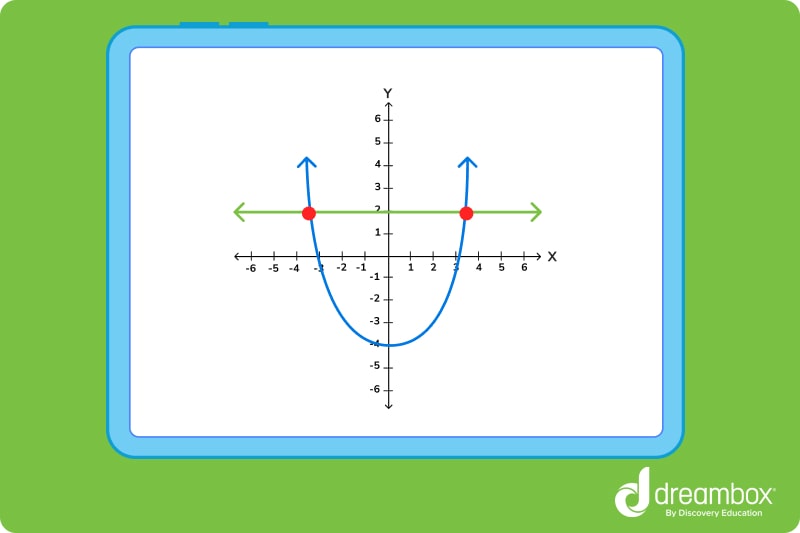
Answer: No, it does not.
Question 2: In the figure below, which angles are adjacent to angle C? Which angle is opposite?
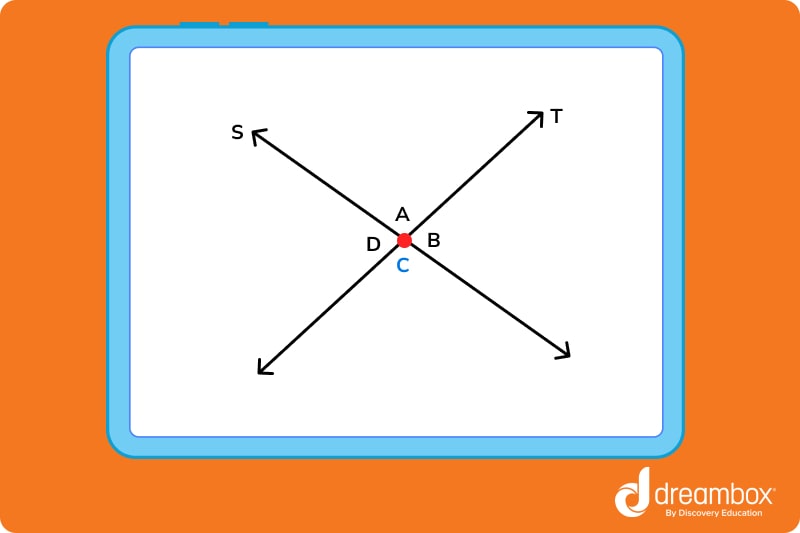
Answer: < B and < D are adjacent to < C. < A is opposite < C.
Question 3: What is the point of intersection of these two lines?
y + 3 = -1x
y = 5x + 9
Answer: The point of intersection is (-2,-1).
Parent guide
Question 1: Although these lines are intersecting, they are not both straight lines. Therefore, these cannot be classified as intersecting lines.
Question 2: Adjacent angles are next to each other. They share a side and a vertex. Looking at the graphic, we can see that < C shares a side and vertex with both < D and < B. Opposite angles are across from each other. < A is opposite < C.
Question 3: To solve this problem, make both equations equal to y. After reordering the first equation, y + 3 = -1x becomes y = -1x – 3. Since both equations now equal y, both equations are also equal to each other: -1x – 3 = 5x + 9. Solve for x to find x = -2. Plug -2 into the first and/or second original equation/s to solve for y. Find y = -1. The final answer is (-2,-1).
FAQs about intersecting lines
There is no intersecting line symbol in math.
To test if two lines are intersecting, determine their slopes. If they have different slopes, they will intersect. If they have the same slope, they are parallel and will not intercept.
A pair of intersecting lines can have any slopes, as long as their slopes are different from each other.
