Fraction Fundamentals
Dive into articles that turn math struggles into successes with engaging content crafted to boost kids’ math skills.
Ever wondered what it means when mom says, “we need to leave in half an hour?” Or how to add funky numbers like ⅙, ¼, and ⅘ together to get a big, whole number? And what is a whole number anyway? Learn all about what fractions are and how to add and subtract them to make all new fractions!
Browse Most Popular Articles:
Browse All Fraction Skills:
Measuring flour for a cake. Taking the temperature outside. Reading a ruler to calculate the length of a picture frame. We use units of measurement every single day! Understanding this crucial math skill begins by learning the metric and customary systems of measurement. Dive into any resource below to learn more.
Simplifying fractions makes them easier to work with – Reducing fractions makes them easier to visualize and work into other math problems.
Have a fear of fractions? While they can be a bit tricky, learning how to add fractions is an important skill to master, and it has a ton of real world applications.
Similar to how we can subtract whole numbers, we can subtract fractions. First, remember the different types of fractions: like, unlike, and equivalent. One important rule: we can only subtract like fractions.
The idea of multiplying fractions might seem daunting and complicated. But, the art of multiplying fractions can be mastered with just three simple steps. No more panicking before that dreaded math exam
Fractions are already parts of a whole number. So, you might be wondering: how can you divide a fraction into an even smaller part—or, for that matter, divide it to turn it into an even bigger part?
We know what numbers are, right? And we know that when you “mix” things together, you’re bringing together two things that may be related, but are not entirely the same thing.
In an improper fraction, the denominator is greater than (or equal to) the numerator. Examples of improper fractions are 9/5, 8/7, and 10/4.
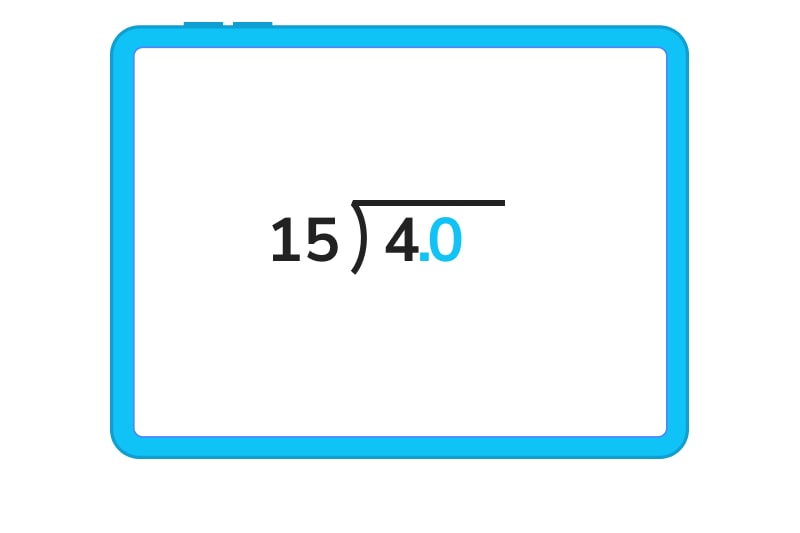
Converting fractions to decimals doesn’t have to be a scary process. In fact, as you get older, it might be even easier than trying to figure out fractions.
FAQs About Fractions
A fraction, very simply, is a part of a whole. So, let’s say you have a whole pizza. A fraction is a single slice of that whole pizza. The pizza itself is made up of 10 slices, and you enjoy 1 slice.
When you look at a fraction, you’re looking at two numbers. The number on the top of the fraction is the numerator – or the slice of pizza – and the number on the bottom of the fraction is the denominator, or all the slices of pizza available.
Typically, students begin to learn about fractions in 1st grade. 1st graders will learn fractions, but only basic ones like ½, ⅓, and ¼. They will typically learn how to recognize fractions by dividing shapes into wholes, halves, thirds, and fourths. As they advance through 2nd, 3rd, 4th, and 5th grade, their lessons around fractions will become more complex, until they are multiplying and dividing fractions on their own.
There are several methods you can use, and it’s always best to talk to your student’s teacher to see if there are ways to support the learning that is already happening in the classroom. However, a good rule of thumb is to make learning fractions visual whenever possible. Folding paper, cutting circles into halves and fourths, and other similar strategies can be very effective.
Simplified fractions are fractions that have been reduced to their simplest, lowest form. For example, 4/16 can be simplified to 1/4.
Want to see that in even more detail. Let’s consider 5/15.
Obviously, 5 is divisible by 5, right? So 5÷5 = 1
And 15 is also divisible by 5. So 15÷5 = 3.
That means 5/15 can be simplified to 1/3.
Grades:
If you’ve ever wondered how to help your 3rd grader with math homework or what your child should know by the end of fifth grade, these elementary math resources are for you. Choose a grade level below to browse math skills and objectives by grade.
