Learning Division
Dive into articles that turn math struggles into successes with engaging content crafted to boost kids’ math skills.
Division can be one of the hardest math skills to master, but it’s super important as students advance to higher-level mathematics. Whether they’re trying to discover how to divvy up pieces of pizza to give to their friends or solving complex problems in high school classes like precalculus and calculus, elementary schoolers will want to start practicing division skills now to make sure they’re ready – both for the classroom and the real world!
Browse Most Popular Articles:
Let’s split up the elements of a division problem!
Discover ways to find the quotient using simple subtraction methods.
Turn your big numbers into smaller ones with long division. Master these easy steps and you’ll be a division wiz.
Tips from a math tutor for parents on how to teach division to struggling students!
Browse All Division Skills:
Like almost all mathematical skills, division starts out simple and becomes more complex as you move throughout school. Let’s take a look at different division skills to make sure we’re prepared at every stage of learning.
Learning how to divide decimals doesn’t have to be complicated, just try not to forget the point.
All About Division
Division is one of the most important math skills you’ll practice, helping you to undo multiplication problems or break off parts of a “whole.” We know it looks complicated, but it really isn’t! You just need to know what signs to look for that tell you when division is needed.
Like addition and subtraction, division uses a few special terms and symbols. Knowing these can help you to work out your problems quickly and correctly.
We know it sounds complicated right now — but with a little practice and this handy guide, you’ll be flying through your math homework in no time!
What is Division?
Division is a process in math that lets you break down a number into multiple, equal parts. Sometimes, you can cut everything down into whole number parts, and, sometimes, you’ll be left with a little leftover, giving you a decimal or fraction for an answer rather than a whole number.
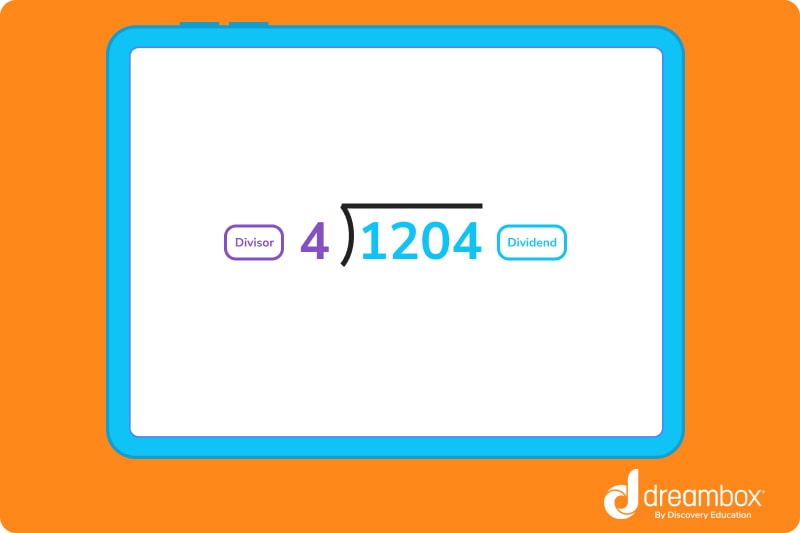
You’ll often see division problems vertically, like this:
It can also be written horizontally: 10 ÷ 2, as 10/2 , or using a division bar: 2⟌10.
No matter how you see it, though, the use for it is always the same. You’re breaking down a number or quantity into smaller pieces.
Let’s take a look at some key terms that’ll help you build your division skills.
Common Division Symbols and Terminology
Division is a simple mathematical operation, but there are still a few terms to know to help you find the correct solution.
Here are the terms you need to know to solve division equations with ease:
Division Symbols
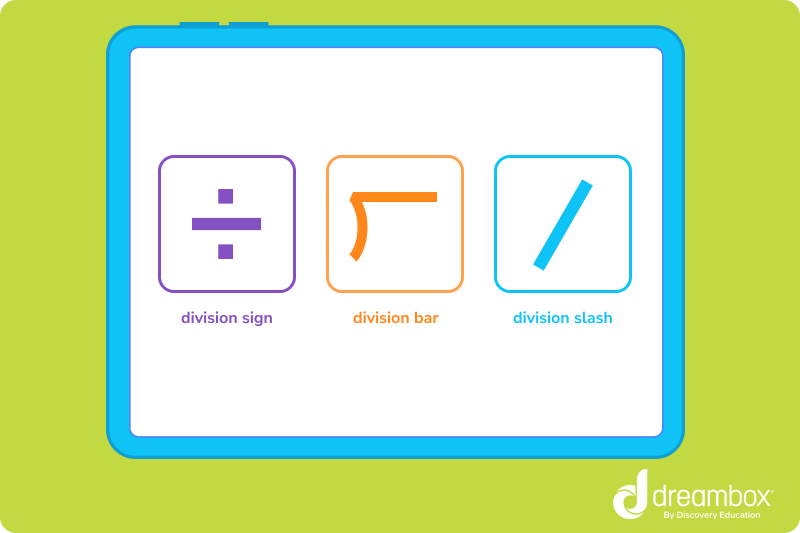
- ÷ — This is known as a division sign, and it tells you that a number needs to be broken down into multiple pieces.
- ⟌ — This is the division bar, and it also means to divide. On the outside of the bar, you’ll see the number determining how many pieces are needed from the whole (the divisor), and the dividend on the inside, which is what you’ll be dividing. The answer goes on the top of the bar.
- ∕ — This is known as the division slash. Generally, the divisor comes first, and the dividend will appear second.
Division Vocabulary
Knowing these terms will help you to know what numbers you’re dividing and how you should set up and read your equations. There are four main terms to know as you work through your arithmetic operations.
- Divisor – The divisor is the number that is determining how many pieces are needed from the whole. For example: in 15 ÷ 3, three would be the divisor. It’s also the number located outside of the bracket when you see a division bar.
- Dividend – The dividend is the number that’s being divided, and it’s found inside the division bar.
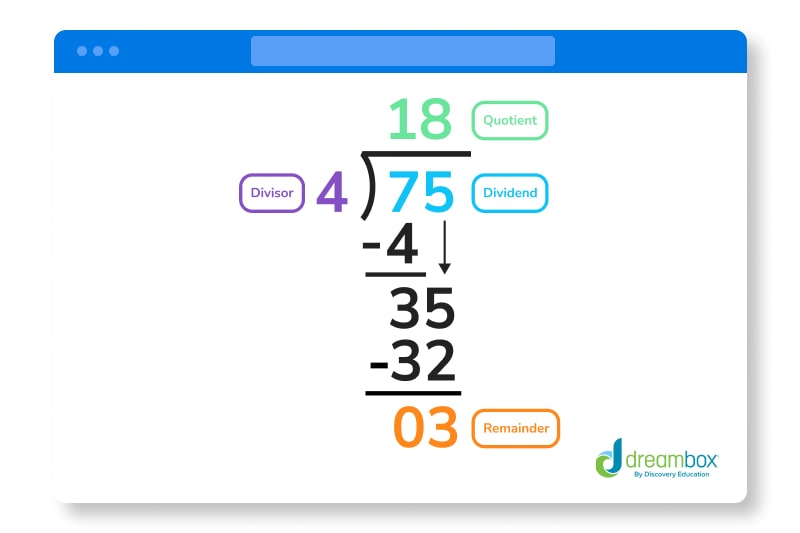
- Quotient – The quotient is your answer, which goes after the equals (=) sign or on the top of the division bar.
- Remainder – In some cases, you’ll have a remainder — which means that the divisor can’t be equally divided into the dividend. The remainder is written to the side of your equation next to the division bar.
Properties of Division
Anytime you see the word “property” in math, know that it’s just a rule to remember as you work through your groups of problems. Here are some of the most important properties of division that you need to know:
- The Division By 1 Property: If a number is divided by 1, the quotient will always be the original number.
- The Division By Itself Property: If a number is divided by itself, the quotient will always be 1.
- The Division By 0 Property: If a number is divided by 0, it’s “undefined” and cannot be solved.
- The Division Of 0 By (Any) Number Property: If a 0 value is divided by any number, you’ll have 0 as your quotient.
Knowing these helpful properties can help you to do basic operations (like division) confidently. Remember — these are division facts, so these properties will always be true…no matter what problem you’re working to find the quotient to!
How to Divide in 6 Easy Steps
Now that you know the terms and properties of your division operation, it’s time to practice your skills. Let’s work the problem below together.
1. Prepare your equation
We know that the problem above can feel overwhelming — so we want to take this moment to remind you that what we’re doing is breaking down a number into smaller numbers (or smaller groups of numbers).
First things first, we have to prepare the equation. Feel free to keep it horizontal, write it vertically, or use a division bar if you’d like. Use whatever method you feel comfortable with.
Remember: The dividend (15) belongs inside the division bar if you choose to use that method.
2. Start with the first digit of the dividend from the left
As we begin to divide, we need to start from the first digit from the left (in this case, 1) and ask ourselves: Does the divisor (3) go into 1 at least once?
The answer here is “no,” so we will then evaluate the first AND second integer (making 15) as a dividend.
We ask again: Does the divisor (3) go into 15 at least once?
Now, the answer is “yes” — we just have to count how many times 3 can go into 15, starting our division process.*
*NOTE: You can do this by using basic arithmetic operations (such as multiplication) to “undo” the problem (i.e., 3 x ? = 15) or counting by threes until you reach 15.
In our case, 3 goes into 15 a total of five times.
3. Divide it by the divisor and write the answer on top as the quotient
Now that we know that 15 ÷ 3 = 5, it’s time to write it into our equation. Go ahead and write 5 behind the equals sign or standing tall at the top of your division bar.
4. Subtract the product of the divisor and the digit written in the quotient from the first digit of the dividend
Now, we have to check our work. We have to ask ourselves: What is 5 x 3? Does it equal our dividend? If it does, you’re golden — you’ve done it!
Do the multiplication, and then subtract your product to ensure that there’s no other steps remaining (like you’d see in the case of a remainder).
In our example, 15 – 15 = 0…so no remainder or further action is needed.
5. Bring down the next digit in the dividend (if possible)
In other problems, if you did have a three or four digit dividend, you might need to bring down the next digit in the dividend, and determine if your divisor divides that number cleanly.
You would then repeat the division process, putting your answer over the third or “next” place above the division bar as part of the quotient.
Next, you would repeat step 4 to determine if more steps in the division process are needed.
In our example, we don’t have to do this, so we will leave it as is. Good work!
6. Repeat
Congratulations! You just broke a large number down into equal, separate parts. It’s time to repeat the process for your other problems.
What is Long Division?
Long division is a form of division that’s used to break down larger numbers and will generally repeat steps 1-6 above at least three or more times.
Browse our long division guide for a deeper dive.
Working with Remainders
What happens when you wind up with a little extra left over, you might ask? While it can look pretty scary, it’s simple to solve.
To do this, you’ll repeat steps one through five above until you get a number that cannot continue to be divided evenly. At this point, you’ll do a few additional steps:
- Determine how many times the divisor goes in to the product of your current answer and the divisor. This won’t be a clean number, and that’s OKAY — that’s what your remainder process is for.
- Complete the subtraction steps. After you get your number, complete the subtraction steps and write your answer below the subtraction bar.
- Do a quick check. If you cannot use your divisor to break your difference down into smaller pieces, that is your remainder. You can note it as: Answer R#.
- For example: In the case of 16 ➗3, we would write the quotient as: 5R1.
When you see that there’s zero left over, or if there is no way for the divisor to divide into the dividend, that means that your problem is solved!
FAQs About Division
Division is important because it helps us split things into equal parts. This can help us share a portion of something equally or help us divide our time during the day so we can accomplish the tasks ahead of us. You’ll use division almost every day as you get older!
- Addend – One of the two numbers you are adding together
- Sum – What you get when you add the addends together
There are plenty of times you’ll use division in your everyday life. Some of the most common ways might be to break up an even quantity of something, determining how much of an ingredient to use, or grouping up items for use.
Division is the inverse of multiplication. This means that it naturally undoes any sort of operation that’s done with multiplication.
The three main parts of division are the divisor, dividend, and quotient.
Grades:
If you’ve ever wondered how to help your 3rd grader with math homework or what your child should know by the end of fifth grade, these elementary math resources are for you. Choose a grade level below to browse math skills and objectives by grade.
