What is an Equation?
An equation is like a sentence in math that shows how two things are equal.
Published:
Jan 2025
Key takeaways
- Equations are everywhere — You’ll need to know how to solve them.
- There are different types of equations — Common equations include linear, quadratic, and polynomial.
- An equation has several components — Each one plays an important role.
Whether you’re figuring out how much money you’ll have after buying a snack or solving complex problems in science and engineering, equations are everywhere. Learning how to work with equations makes you a better problem-solver and gives you tools to tackle challenges you may face in school and in life.
Definition of an Equation
An equation is like a math sentence that shows how two things are equal or balanced. It’s made up of numbers, symbols, and letters that represent unknown numbers.
Here’s an example of an equation: 5 + x = 7. It tells us that 5 + the mystery number (x) equals 7. Your job is to solve the equation and determine what x is. In this simple equation, x would be 2, because 5 + 2 = 7.
Get more practice on odd and even numbers with DreamBox Math
DREAMBOX MATH
Get started for FREE today!

Types of Equations
There are lots of types of equations. Each one helps you solve different problems. Let’s take a look at these types, from linear to quadratic and beyond.
Linear Equations
A linear equation is a special kind of equation that makes a straight line when you graph it. Typically, you’ll learn about these in 8th-grade math.
Linear Equation Example: 2x+5=13
Quadratic Equations
A quadratic equation is a type of equation that involves squaring a number, which means multiplying the number by itself. When you graph a quadratic equation, you get a curve called a parabola, which can look like a smiley face or a frowny face.
Quadratic equations usually look like this: ax2 + bx + c = 0. The a, b, and c are always numbers.
You might look at the equation and wonder how or why you’d use it in real life. Quadratic equations are used to calculate things like the curves in a design or even the speed of an object.
Quadratic Equation Example: x2+5x+6=0
Polynomial Equations
A polynomial equation is made of numbers and variables (like x) that are added, subtracted, or multiplied by each other.
The variables are raised to an exponential power, like x2 or x3. A polynomial equation can have many parts, but the highest power tells us what kind of polynomial it is.
For example, if the highest power is 2, it’s a quadratic equation; if it’s 3, it’s a cubic equation. You may learn about these in 8th grade and revisit them in later grades, too.
Polynomial Equation Example: 2x3−4x2+3x−5=0
Differential Equations
Imagine riding your bike and your speed changes throughout the ride. To measure those changes in speed, you’d use a differential equation, which is a math equation that shows how things change. Instead of talking about how something is at one moment, it shows how things change over time.
For example, if you’re moving faster or slower, your speed is changing. The rate of change of your speed (how quickly your speed is changing) is important. A differential equation helps us figure that out.
Typically, you’ll learn about these things if you take calculus in high school.
Differential Equation Example: dy⁄dx+3y = 6
Integral Equations
In math, an integral means adding up lots of little pieces together to get a total. So, an integral equation is an equation that involves an integral, which is just a way of adding up things over time or space.
Think about this: If you want to know how much water has flowed into a swimming pool over the last hour, and you know how much water is flowing in each minute (but it’s changing every minute), you would add up all those little amounts to find the total amount of water that came in.
You’ll also typically learn about these when taking high school or college calculus.
Integral Equation Example:
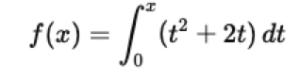
Start Your Free Trial
See how DreamBox can help your sixth grader with math by signing up for a free trial today.
No credit card required!
Components of an Equation
Several components make up an equation. Let’s learn more about each one and the role they play.
Variables
Variables are like the mystery part of an equation — they stand for numbers we don’t know yet and are usually represented by letters such as x, y, or z. When you’re solving an equation, your job is to figure out what number these letters represent.
Look at the simple equation x + 5 = 10. To figure out x, you’ll need to subtract 5 from both sides, which leaves you with x = 5.
Constants
Constants are like the fixed or steady parts of an equation.
They’re numbers that don’t change, unlike variables, which can vary or change. Think of constants as the strong, reliable foundation of a house. No matter what happens in the equation, constants remain the same and keep their value.
For example, in the equation y = 2x + 3, the constant would be 3. It’s not going to change even if the values for x and y change. Constants provide stability and help us understand how equations work.
Operators
Operators are like action words or symbols in math that tell you what to do with the numbers and variables in an equation. They are the special symbols that explain how to combine or relate the parts of the equation, kind of like giving instructions in a recipe.
The most common operators are addition (+), subtraction (-), multiplication (× or *), and division (÷ or /).
In the equation 3x + 4 = 10, the operators are “+” and “=”. Here’s what they tell us:
- The “+” means to add 4 to whatever value you get from multiplying 3 by x.
- The “=” is the equal sign, which tells us that the left side of the equation should be the same value as the right side.
Operators help us understand how to solve equations. Just like in stories where verbs show actions, operators in math show us the actions we need to perform with numbers or variables.
Functions
Imagine a vending machine where you put in a coin (input) and get a candy bar (output). Similarly, with functions, you put in a number, follow the function’s rule, and get another number out.
A function is often written as f(x), where x is the input. The f names the function and tells you how to transform the input to get the output.
Let’s look at an example: f(x) = 2x + 3. It tells you to multiply whatever number you put in for x by 2, then add 3. So if you put in 4, the function gives you:
- 1. Multiply 4 by 2, which is 8.
- 2. Add 3, making it 11.
- So, f(4) = 11.
Functions always operate with the same rule, ensuring consistent and predictable results.
Balancing an Equation
Balancing an equation is like having a seesaw at the playground where both sides need to be even for it to stay level. In math, balancing an equation means ensuring both sides of the equation have the same value.
Here’s a simple example: look at the equation x + 3 = 7.
The goal is to determine what x needs to be so both sides are equal. To find out what x is, we need to get x all by itself. Since 3 is being added, do the opposite operation and subtract 3 from both sides.
By subtracting the same number from both sides, we’ve kept the equation balanced, just like making sure both sides of the seesaw have the same weight.
Real-World Applications of Equations
Equations are super useful tools in all sorts of places, just like a Swiss Army knife with many gadgets.
- Science: Equations help us understand the world — like Einstein’s famous equation of E = mc2 which explores how matter and energy are related.
- Engineering: Equations help build things like bridges, making sure they’re strong and won’t collapse.
- Economics: Equations help people figure out prices and how money moves around.
Even in everyday life, we use equations without even realizing it, like when we calculate how much time it takes to get to school or when we figure out how much a few candies cost.
Conclusion
Equations are an important part of our lives, and we use them every day, whether we realize it or not. As with most math concepts, practice makes perfect! It takes time and practice to get the hang of solving equations.
If you have questions while you’re working on your next equation, let DreamBox help!
FAQs about equations
The difference between an equation and an expression is a bit like the difference between a complete sentence and a sentence fragment.
An expression is a math phrase that shows a part of a calculation but doesn’t have an “equals” sign. It’s a group of numbers, variables (like x or y), and operators (+, -, ×, ÷) that doesn’t complete a thought. For example, 3x + 2 is an expression. It tells you to multiply a number by 3 and add 2, but it doesn’t tell you what that’s equal to.
On the other hand, an equation is like a full math sentence because it includes an equal sign (=). An equation shows a complete thought by saying one thing equals to another. For instance, 3x + 2 = 11 is an equation. It’s telling you that when you plug in a number for x, the left side will balance the right side, which in this example is 11.
Equations are what you solve to find out those mystery numbers.
Remember, think of an equation as a complete thought.
An example of an equation could be 7x + 2 = 37. To solve it, you’d subtract 2 from each side, leaving you with 7x = 35. Divide each side by 7 and you’re left with x = 5.
A formula is a special type of equation that shows you how to calculate something.
For example, the formula for the area of a rectangle is Area = Length x Width. This formula tells you exactly how to find the area when you have those two numbers.
An equation is a math statement with an equal sign that shows two things are the same. Equations can be used to solve problems or figure out unknown numbers, like in the equation 7x + 2 = 37.
This isn’t a general rule like a formula, but a specific problem you’re trying to solve.
Think of a function like a vending machine. You put something in and out comes a result.
If a soda costs $1, you put in $1, and you’ll get the same result each time. That’s how a function operates.
An equation needs to be balanced, like a scale. It uses an equal sign to show the two sides are balanced, and you use them to find unknown values to make the scale balance perfectly.
Take at home math practice to the next level
Empowering parents and educators to make math practice more impactful. Plus, your kids will love it.


