Learning Addition
Dive into articles that turn math struggles into successes with engaging content crafted to boost kids’ math skills.
More, more, more! Addition is all about making more of something, whether it’s making a number bigger or giving someone more of what they need or want. It’s also a crucial skill to understand if you hope to become a math expert. With a little bit of practice and a whole lot of determination, you’ll get addition down in no time!
Browse Most Popular Articles:
Two plus two equals __? Learn what the sum is in math. (Hint: it’s what you get when you add two numbers together!)
Repeated addition is the foundation of multiplication. Learn more about repeated addition in this guide.
It’s very simple — when you add zero to any number, the result is always the number itself. Let’s dig in to learn more about the identity property of addition.
The associative property tells us that no matter how we arrange three or more numbers in an equation, we’ll always get the same sum. But how and why? Let’s take a closer look.
Browse All Addition Skills:
Like subtraction, addition starts simple but gets more involved as you climb through 1st, 2nd, and 3rd grade. You can learn different skills to solve your addition problems with ease — and prepare for addition in the real world! Let’s take a closer look at the fun things you can do with addition.
Find out how addition can help you understand how to multiply numbers together.
Learn about this foundational concept when tackling addition problems.
See how grouping digits can help us break down an addition equation!
All About Addition
Aside from simple counting, addition is the most basic and fundamental mathematical skill you can learn. Before you can subtract, multiply, and divide, you need to be able to combine numbers together through the power of addition. It’s actually a skill most people use daily, whether they are paying bills, cooking a meal, scheduling different activities, or just figuring out how much candy they’ve eaten in a day.
No matter how much math you plan on doing in your life, make no mistake – everybody needs to know addition! Let’s take a deeper dive into this valuable skill.
What is addition?
Addition is all about finding the sum, the combined value of two or more numbers. We call numbers we are adding together “addends”, but most people hardly ever use that term.
To find the sum of some addends, you take a number like 5 and then another number, like 7, and try to figure out what number you get if you combine those two. In this case, 5 + 7 will get you 12.
The + symbol is called the “plus sign,” and it is the symbol we use to show that we need to add two numbers together. We use an equal sign, which looks like =, to show what the value of the added numbers is. Get used to these symbols – you’re going to be seeing them a lot!
How to add two numbers together
There are a few options to help you find the sum of numbers. Depending on how your mind works, some of these options will make more sense than others. Just feel free to try them all out and see what works best for you.
Let’s get started looking at how to find the sum of two numbers. We’ll keep things simple for now.
Addition using a number line
A number line is a simple visual representation of numbers counting from 1 to whatever value you’d like. An easy way to figure out a sum is to use a number line.
Start by looking at your addition problem. Let’s look back at the example from earlier, 5 + 7. Look at the first number in the problem, 5, and count that many spaces on the number line. You’re halfway done already!
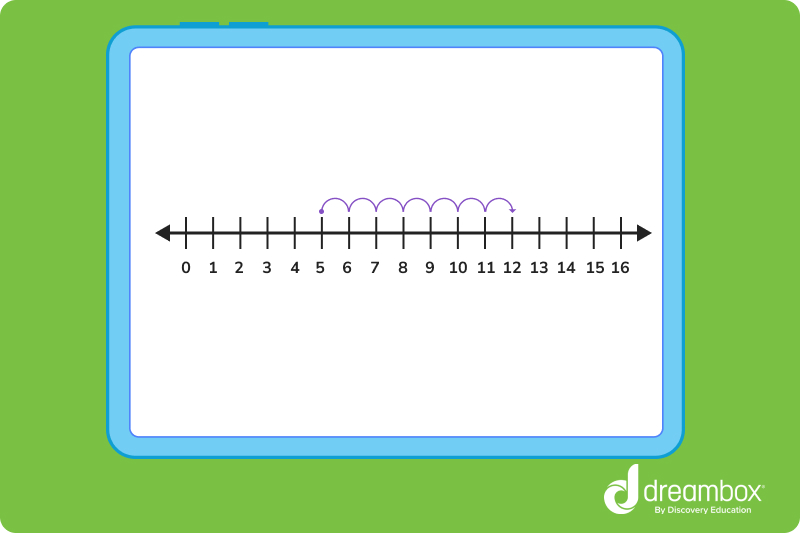
Now, look at the second number in the problem, which is 7. Keeping your place on the number line that you found with the first number, count out 7 more spaces on the line. 5, 6, 7… all the way to 12!
Guess what? You just found the sum of 5 and 7!
Addition using your fingers
If you are trying to find the sum of smaller numbers and you don’t have any paper handy for a number line, you can just use your fingers. Let’s do this with a new addition problem, 3 + 6. Start with your hands balled up into fists. As you count out the numbers, you will hold up fingers to help you keep track, just like with spaces on a number line.
Hold out your left hand. We’re going to start with the first number again, which is 3. Count it out — 1, 2, 3 fingers. Great, now let’s handle that second number, 6. On the left hand, keep those 3 fingers up but start counting to 6 using the fingers you haven’t raised yet.
1… 2…
Now all the fingers on your left hand should be up. But wait, you are all out of fingers! Well, you can move onto your right hand. Keep counting. You can get all the way to 6 by using the 2 fingers you had on your left hand and 4 on your right. Now, count how many fingers you are holding up. You should see 9 fingers total, which is the sum of 3 and 6!
For sums greater than 10, you will need to “carry” the one mentally and start over by lowering your fingers. We’ll talk more about “carrying” in the next section.
Addition using carrying
Eventually, you will need to start adding up larger and larger numbers. That means eventually the number line will get a little too long, and you will quickly run out of fingers (and toes!) for counting. You will need to rely on regrouping or carrying numbers to handle larger addition problems.
Let’s say you need to find the sum of 24 and 32. Things are about to get a little tricky, so let’s try to arrange these numbers to make things easier to understand. We will stack them up on top of each other so we can handle one part of each number at a time. It will look like this:
Notice how the larger number is on top. It doesn’t matter which number goes on top in addition, but putting the larger number up there is a good habit to get into because of how things like subtraction work. We’ll worry about that later, though.
Now that we have the numbers lined up, we are going to add one column at a time, starting with the ones place. Let’s start by adding 2 and 4 together. For this you can try using the number line or your fingers again. 2 + 4 = 6, so let’s write a 6 down below the 2 and the 4. Like this:
Drawing a line between the numbers you are adding and the sum you are working on will help you keep the numbers straight.
Now that we have added the numbers in the ones place, let’s move onto the tens. Add up 3 and 2 with your number line or fingers and write it below in the tens space next to the 6. 3 + 2 = 5, so let’s drop that down below.
And there you have it! 32 plus 24 equals 56.
It does get a little more complicated sometimes, though.
Take a look at this problem next. What is 27 + 15?
Let’s set that up just like before.
Just like before, we will start with the ones place. 7 + 5. That will get you to 12, but here’s the problem. You can’t just write 12 down below like you did with the 6 from the last problem because that would take up the spot where you would add the 2 and the 1 in the tens place, right?
What you have to do is “carry” the 1 in the 12 you got from adding 7 and 5. That “1” in the number is basically just 10. You can think of 12 as being 10 + 2. That means you can put the 2 below just like before, and move the 1 to above the 27.
It’s easier to just see it in action:
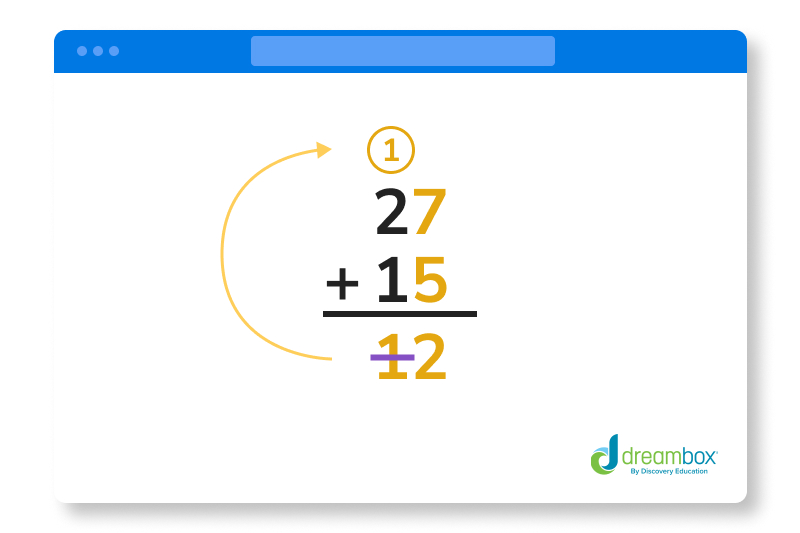
Remember, that 1 up there is basically just a 10, so you are adding 3 numbers now, but it’s nothing you can’t handle. Let’s add up those numbers in the tens spot now. 1 + 2 + 1. 1 + 2 will get you 3, and then you add 1 to that to get 4.
Write that down below.
And there you have it! 27 plus 15 equals 42. You can use the “carrying” technique as many times as you need to in an addition problem. Any time a column adds up to more than 9, you will carry the 1 in the tens place and place it over the next column.
Here’s an example of this process going into the hundreds place.
Add up the numbers in the ones first. 7 + 5 = 12, so the 1 is carried.
Time to add up the numbers in the tens place.
Note that if you were adding up numbers that had hundreds, you would need to carry the 1 again until you run out of columns.
More advanced ways to work with addition and addition examples
As you might expect, addition can get even more complex since there are so many different things you can add. Fortunately, you won’t have to worry about more complicated addition until later in school, but it is good to go ahead and start thinking about these ideas.
Adding two fractions
Especially with things like cooking and baking, with 1/2 a teaspoon here and 1/2 a tablespoon there, you’ll need to figure out how to add fractions together or your cake might turn into a muffin.
To find the sum of two fractions, there are a few steps you have to follow:
- Check to see if the fractions are “like” fractions. Like fractions have the same denominators (the numbers on the bottom of the fraction). If they are, you can skip to bullet number 4. If they’re not like fractions, move on to the second bullet.
- Find the lowest common denominator. When the fractions are unlike, we need to find the lowest common denominator, or LCD. We’ll learn how to do that below.
- Make the two fractions “like” fractions. Convert each fraction into an equivalent fraction, or like fraction, having the denominator equal to the LCD found in the last step.
- Add the numbers on top. After both fractions are like fractions, add their numerators, or the number on top.
- Make it simple. Finally, reduce the fraction to the simplest form if needed.
Let’s see this in action! If a recipe calls for 1/2 cup sugar and 2/3 cup milk, how many cups do you have in total?
First, we know that the fraction for sugar = 1/2
Second, we know that the fraction for milk = 2/3
So we are trying to find out 1/2 + 2/3 = ?
The LCD of 3 and 2 is 6. How do we know this? Well, for this part, you need to know some multiplication, which is a skill you will learn more about later, but just in case you are a little ahead, here’s what that looks like.
To find the LCD, multiply the two denominators together. You will also need to multiply the numerators (the numbers on top) by the denominators.
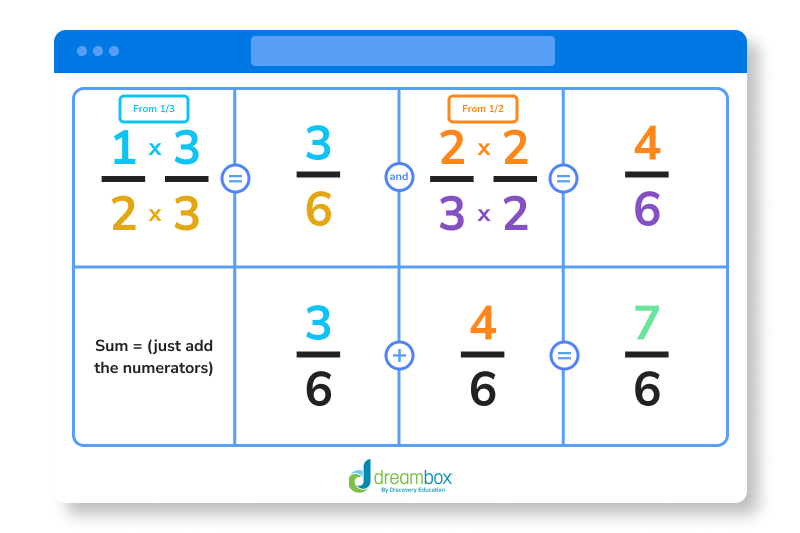
There you have it! 1/2 + 2/3 = 7/6
Adding two decimals
To find the sum of two decimal numbers, there are a few steps that you have to follow:
- Convert unlike decimals into like decimals. This is easier than making fractions “like”.
- Arrange the numbers carefully. Place the decimal numbers so that the tens digit is below the other tens digit, the ones below the ones, the decimal point below the decimal point, and so on. This is just an extension of how we arranged the numbers when learning about carrying the 1 earlier.
- Add the numbers up. Use your carrying skills when you have to.
- Make sure you put the decimal in the right place. Place the decimal point in the sum, or the answer, right below the decimal point in the original decimal numbers.
Time to see this in action, too!
Let’s find the sum of 2.36 and 6.721.
We will first need to convert both the decimal numbers into like decimals by adding zeros to fill in the missing places so that each number has the same number of digits behind the decimal. 6.721 has 3 digits behind the decimal, but 2.36 only has 2. Just add some zeros to make them even, which will make 2.36 into 2.360. This doesn’t change how much the number is, but it will make adding much easier.
Next, add them like whole numbers, moving from right to left, carrying the 1 if and when needed. Don’t forget to put the decimal in your answer!
The total is 9.081!
FAQs About Addition
There aren’t as many terms you will need to know to understand addition as there are to understand subtraction. You need to know two basic terms to understand the definition of addition:
- Addend – One of the two numbers you are adding together
- Sum – What you get when you add the addends together
There are plenty of strategies you can use to solve addition problems. Some of the most common include using a number line, counting on your fingers, visualizing the problem (turning each addend into a picture so you can ‘see’ how many you have when you put them together), and more. Explore these strategies in the Skills section above.
You will begin to practice addition in kindergarten. You might receive three blocks, and your teacher asks you to take two more blocks. How many blocks do you have now? You will start to practice addition problems in first grade, then get into more advanced problems in 2nd and 3rd grades.
All the time! You will use addition to predict how much money you will have after you get paid, how many items you will need for projects and hobbies, how many RSVPs you have received for a birthday party, and so much more! It’s one of the most important skills you can learn.
Grades:
If you’ve ever wondered how to help your 3rd grader with math homework or what your child should know by the end of fifth grade, these elementary math resources are for you. Choose a grade level below to browse math skills and objectives by grade.
