What is Volume in Math?
Calculating the volume of objects has many real-world applications. Students use specific formulas to calculate the volume of three dimensional shapes.
Author
Katie Wickliff
Published:
Oct 2024
Key takeaways
- • Volume refers to the amount of space an object takes up.
- • Volume formulas vary by shape.
- • When calculating the volume of a circular shape, use “pi,” which is approximately 3.14
Whether you’re measuring the ingredients to bake a cake, adding potting soil to a gardening bed, or simply filling your water bottle before a hike, knowing how to measure volume is an essential part of our daily lives.
In this article, we’ll cover the basics of volume and include the formulas to calculate the volume of common shapes. We’ll also include practice problems for each type of shape, to give your student practice using these formulas. For even more practice, head over to DreamBox’s award-winning math app. Let’s get started!
Table of contents
What is Volume?
Simply put, volume is the measurement of how much space something takes up. In a three dimensional (3D) object, such as a pyramid or cone, volume is also often referred to as “capacity.” In a two-dimensional object, volume is known as “area.”
How to find volume
Students learn how to calculate volume by using equations. These equations vary by shape. When your student is first learning to calculate volume, they’ll start by learning to calculate the volume formulas of common 3D shapes, such as these:
Volume of a cylinder
To calculate the volume of a cylinder, we need to know the height of the cylinder and the radius of the base. We also need to know the approximate value of “pi,” a measurement used with circular shapes.
Pi= 3.14 which is represented as π in formulas.
Volume= πr2h
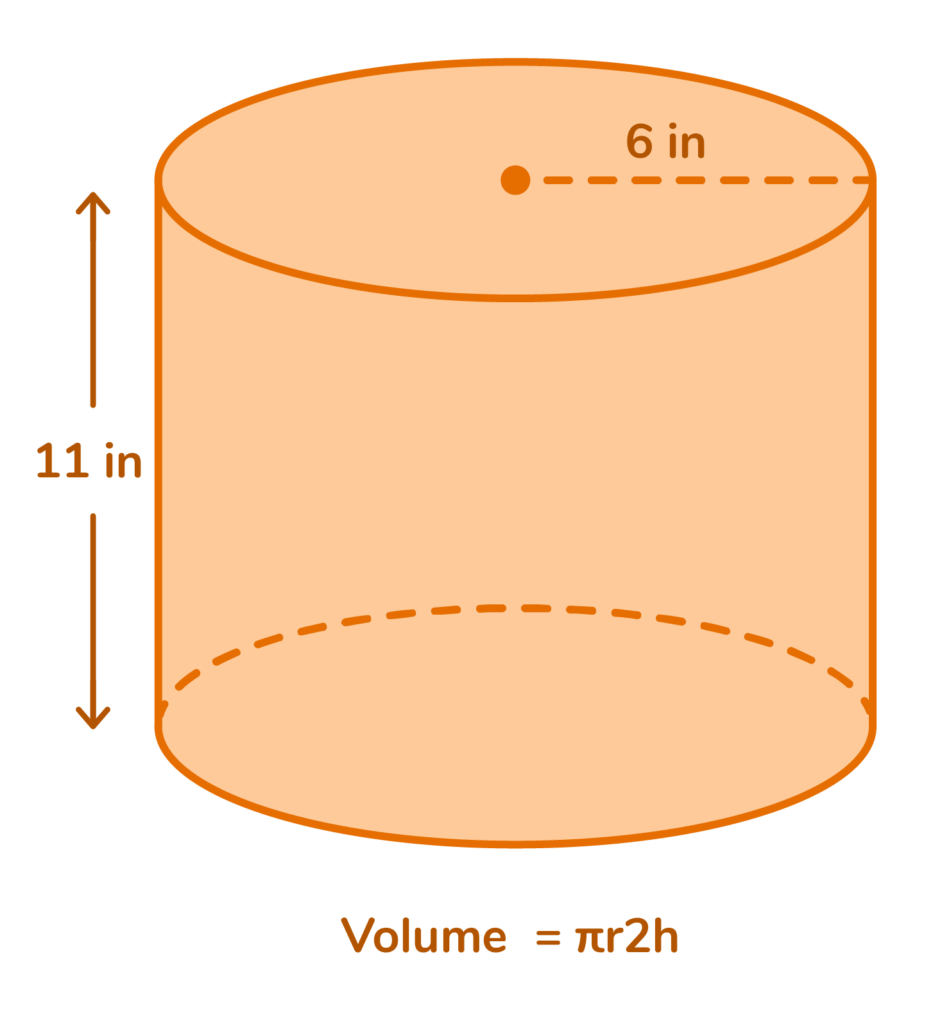
In this example, the radius “r” is 6 inches, and the height “h” is 11 inches.
V= π (6)²(11)
V= π (36) (11)
V= π 396
V= (3.14) (396)
V= 1,243.44 in³
When working with volume, we always use cubic unit measurement, which is represented by “³”
Volume of a Cone
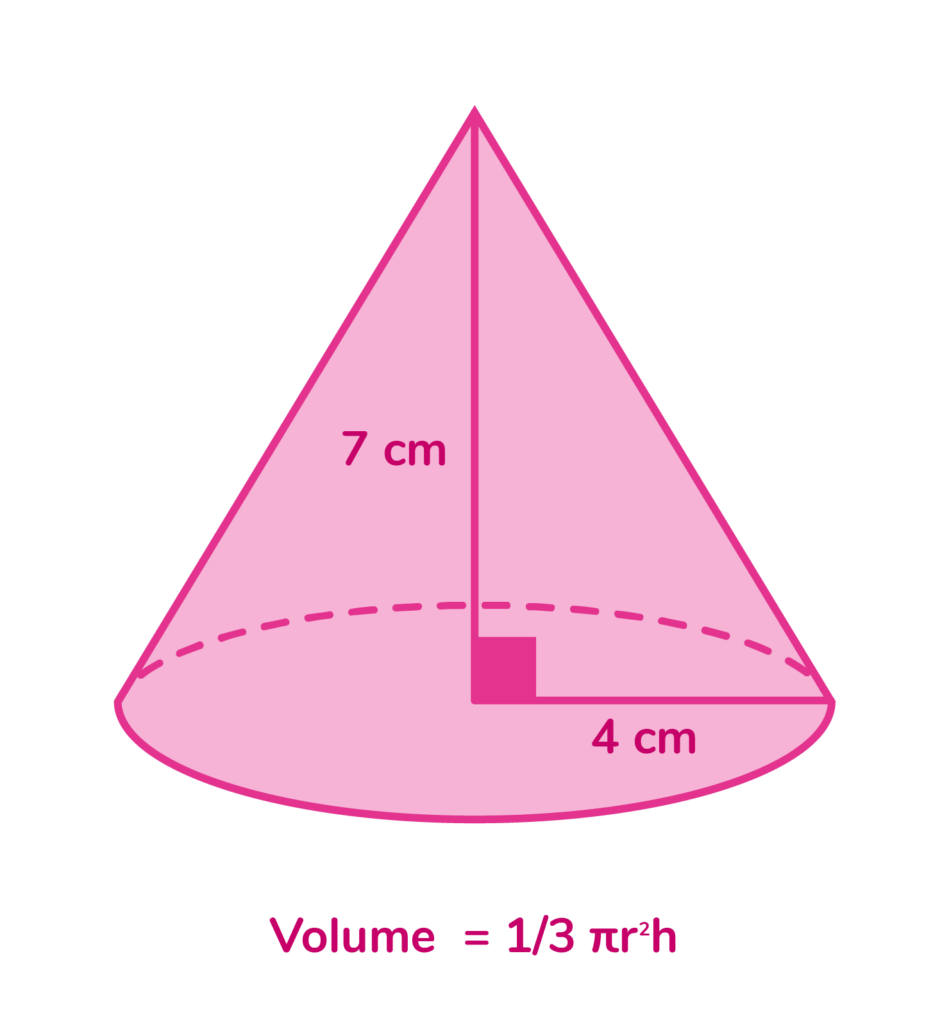
To find the volume of a cone, we need to know the height and the radius of the base. Just like with the volume of a cylinder (shown above) we also need to know the approximate value of “pi”.
To find the volume of a cone, we use this formula:
Volume= ⅓ πr²h
Volume of a Sphere
When calculating the volume of a sphere, we need to know the radius. Just like with cylinders and cones, we also need to know the approximate value of Pi.
To find the volume of a sphere, we use this formula:
Volume = 4/3 πr3
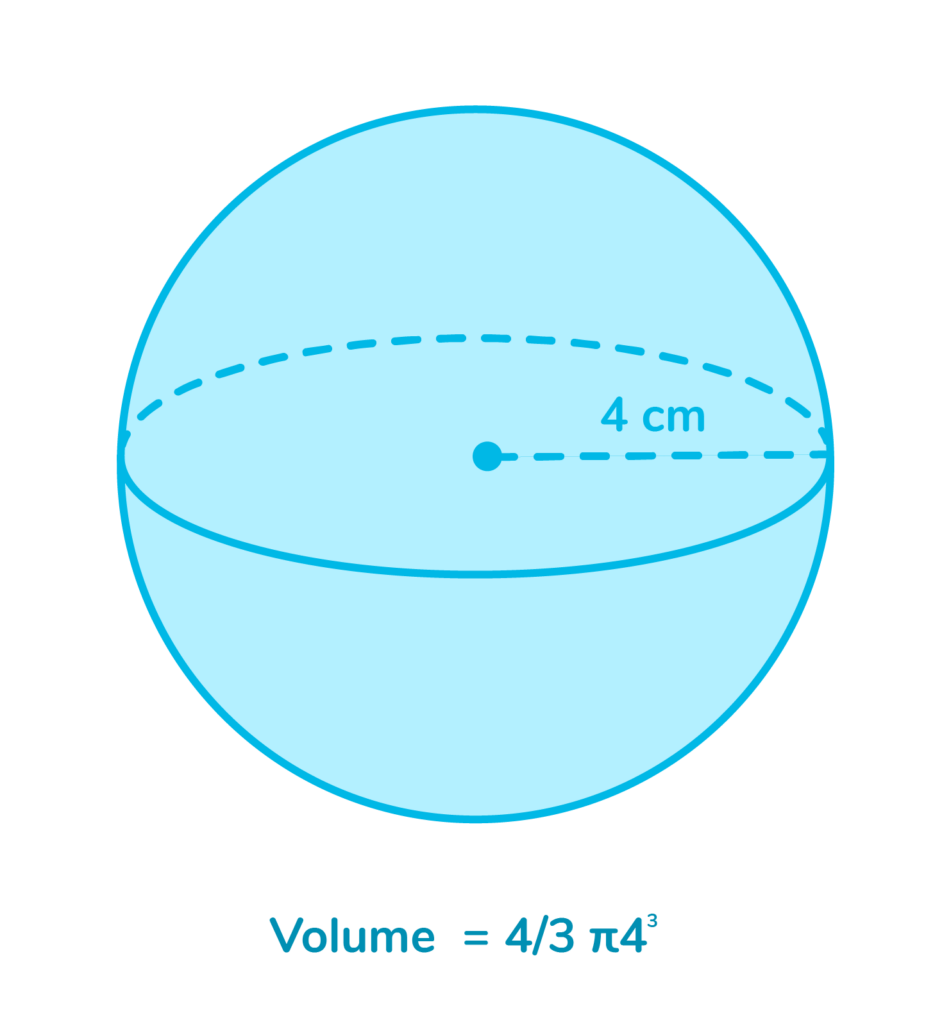
In the example above, the radius is 4 cm.
Volume = 4/3 π4³
V= 4/3 π64
V= 4/3x 64xπ
V= 85.33π
V= 267.94³
Volume of a Rectangular Prism
Volume= 1 x 3 x 2
Volume= 6 ft³
Practice Problems
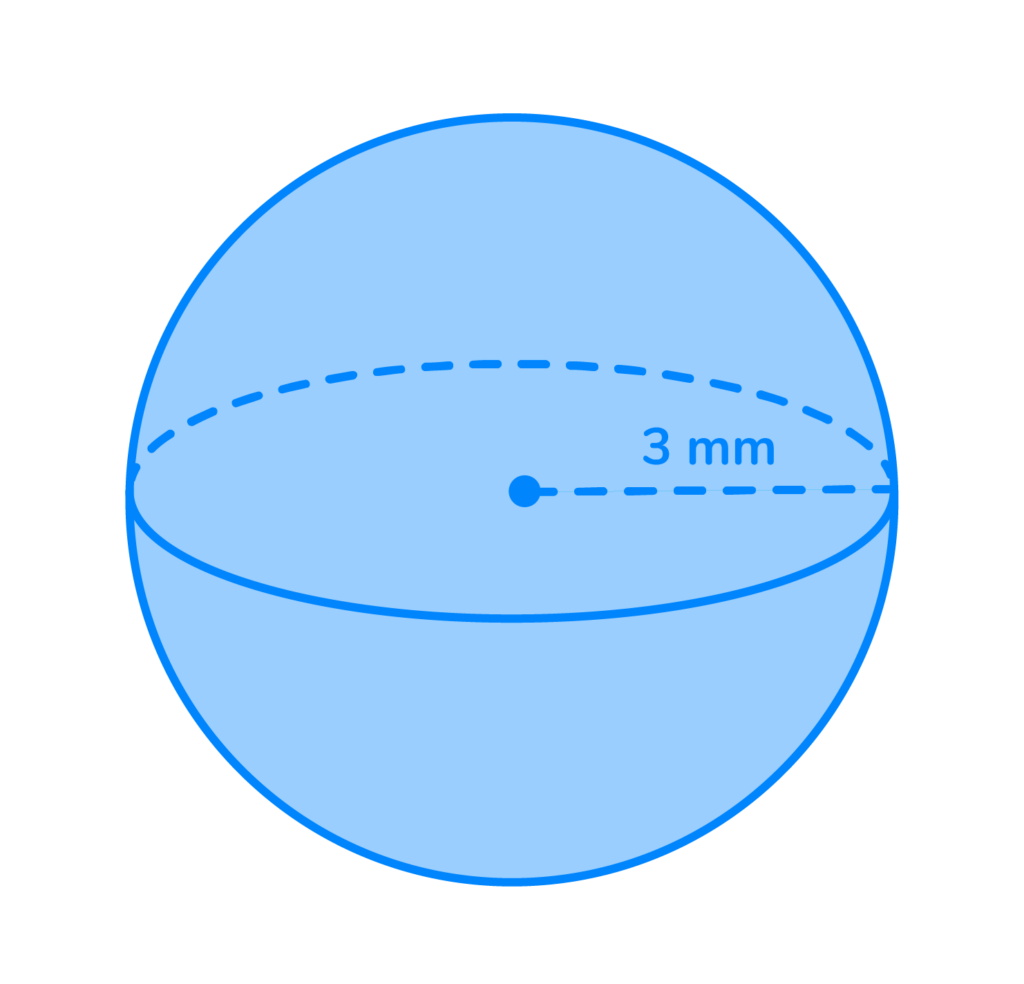
1: Find the volume of the sphere. Use 3.14 for π.
2: Find the volume of the cone. Use 3.14 for π.
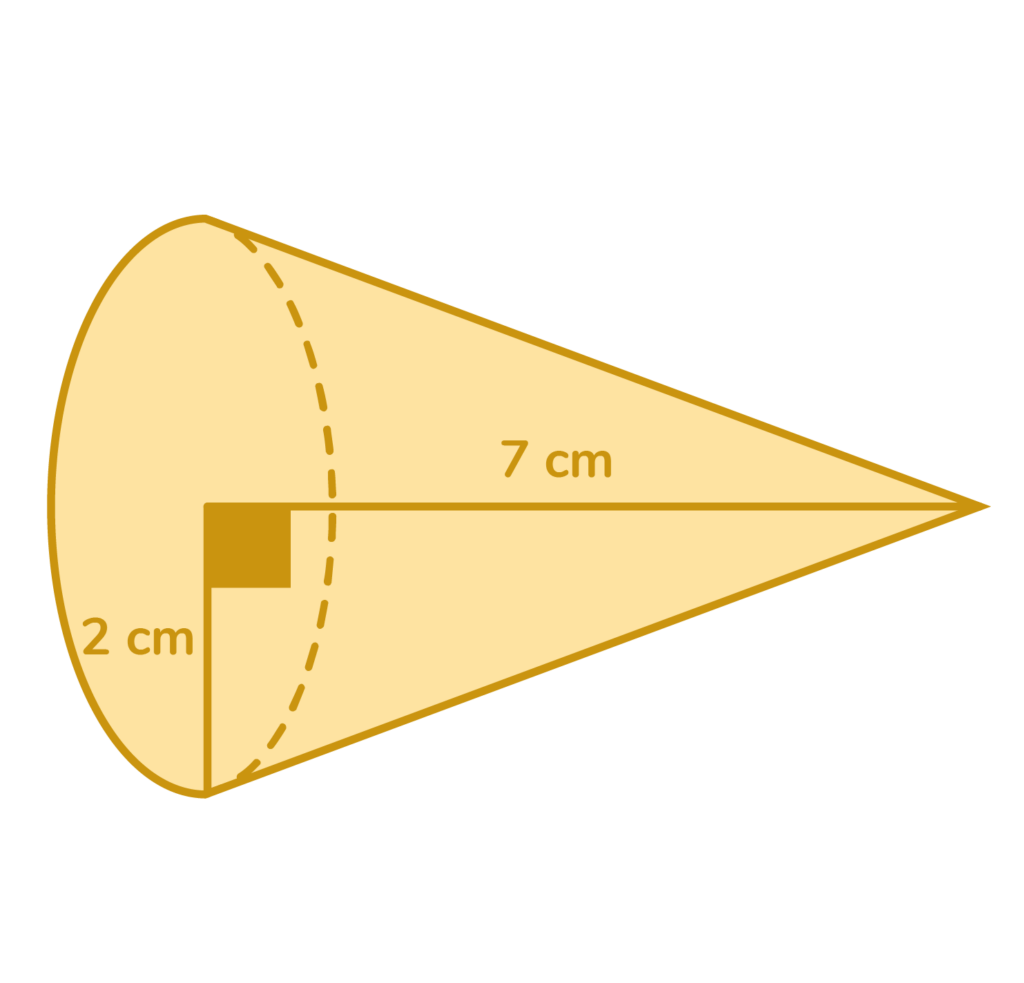
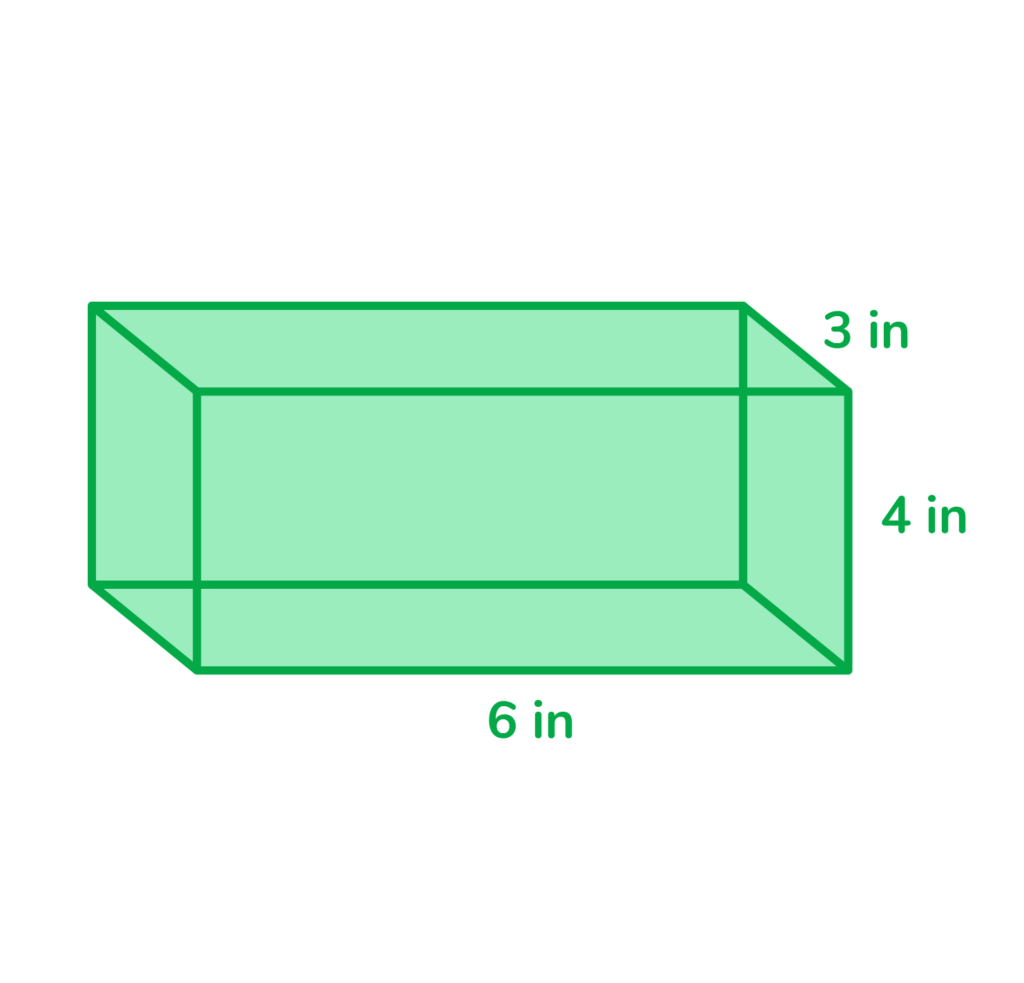
3: Find the volume of the rectangular prism.
4: A drawer is 4 feet long, 2 feet wide, and 3 feet high. What is the volume of the drawer?
Answers
-
1.
- Volume= 4/3π3³
Volume= 4/3π27
V= 4/3 x 3.14 x 27
V= 113.04mm³ -
2.
- V= ⅓ π (2)²(7)
V= ⅓ π (4) (7)
V= ⅓ π 28
V= (⅓)(3.14) (28)
V= 29.3 cm³ -
3.
- Volume= 4 x 6 x 3
V= 72in³ -
4.
- V= 4x2x3
V=24ft³
FAQs about volume
The definition of volume in math is the amount of space an object takes up.
We measure volume by using formulas that differ based on the shape of the object.
Volume formula differs based on the type of shape. When measuring the volume of a cylinder, use the formula v= πr²h. To find the volume of a cone, use the formula volume= ⅓ πr²h. To find the volume of a rectangular prism, use the formula v= l x w x h. To find the volume of a sphere, use the formula v= 4/3 πr3
